| x + 5 | 3 a |
–2 y – 5 +
z |
After completing this section, you should be able to:
In module 1, you were introduced to integers, fractions, and decimals. Numbers such as these can be defined as constants because their values remain constant, that is, they do not change. For example, the value of the decimal 2.56 always is exactly 2.56.
Perhaps the most important characteristic of mathematics is that it is a science of patterns. Describing patterns is often made easier by using a letter to represent all the numbers that fit a specific pattern. We call such a letter a variable because its value varies as it represents different values in the pattern. For example, if we want to add the constant 5 to some numbers, we might write:
0 + 5
1 + 5
2 + 5
3 + 5
.
.
.
continuing indefinitely
This is a pattern, and for this example the numbers 0, 1, 2, … fit the pattern. We can communicate this pattern by using a letter, such as x, to represent the numbers. We would write:
x + 5
to say that we are adding some number to 5. Notice that the value of the variable changes, in contrast to the value of the constant, which remains unchanged. Using variable notation is a primary goal of learning algebra.
A combination of constants and/or variables and arithmetic operators is called an algebraic expression, or simply an expression. Here are some examples of expressions:
| x + 5 | 3 a |
–2 y – 5 +
z |
When a number and a variable are multiplied together, we can simplify the notation by just writing the number and variable next to each other, with no operation sign between them. In the examples above, the last two expressions can be written as:
| 3a | –2y – 5 + z |
This rule also applies when two variables are multiplied together. Thus,
xy means
x
y. The implied multiplication operation is also true for any number of
constants and variables multiplied together. Thus, 7abc
is the same as 7 a
b c.
In module 1, section II, you learned about exponential notation as a shorthand for repeated multiplication. For example:
25 = 2
2 2
2 2
The meaning of the exponent remains the same when the base is a variable. Thus:
x5 = x
x x
x x
or x x x x x
In part B above, you saw that the variable x in the expression x + 5 could represent different numbers. The value of the expression depends on the value of x. Replacing a variable in an expression by a number and then finding the value of the expression is called evaluating the expression. When finding the value of an expression, remember to follow the order of operations given in module 1, section II.
Here are some examples showing how to evaluate expressions.
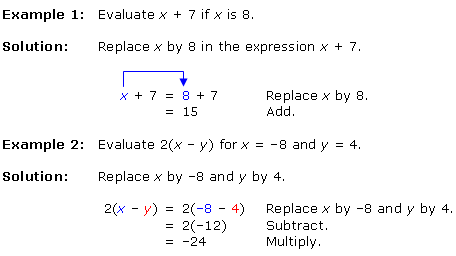
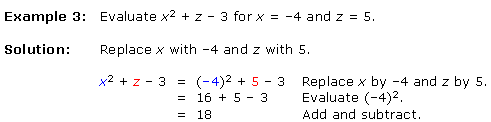
In Example 3, note that we placed parentheses around the base of –4 to ensure that the exponent applies to the negative sign.
 |
Now look at this animation showing how to evaluate expressions. |
To aid us in solving problems later, we now practice translating word phrases into equivalent math statements, or algebraic expressions. Certain key words and phrases suggesting addition, subtraction, multiplication, or division are listed below.
| Addition | Subtraction | Multiplication | Division |
|
sum plus added to more than increased by total |
difference minus subtracted from less than decreased by less |
product times multiply twice of double |
quotient divided by into per |
When you are first learning the process of translating word phrases into algebraic expressions, it may help to write the word phrase on one line, then show the translation immediately below each part of the phrase, as shown in the examples below.
Example 1: This example shows how to translate a word phrase involving addition into an expression.
Example 2: This example shows how to translate a word phrase involving multiplication into an expression.
Example 3: This example shows how to translate a word phrase involving subtraction into an expression.
Hint for Subtraction
Remember that order is important when subtracting. Study the order of constants and variables below.
| Phrase a number decreased by 5 a number subtracted from 5 |
Translation x – 5 5 – x |
Example 4: This example shows how to translate a word phrase involving multiplication and addition into an expression.
After completing this section, you should be able to:
In module 1, we discussed natural numbers, whole numbers, integers, fractions, and decimals, and how to perform arithmetic operations on them. In this section, we will discuss rational numbers, irrational numbers, and real numbers. Then we will explain how these types of numbers relate to each other. But before we begin, we must define a set.
A set is a collection of objects, each of which is called a member or element of the set. A pair of brace symbols { } encloses the list of elements and is translated as the set of or the set containing. For example, the set of numbers 2, 4, 6 can be written as {2, 4, 6}.
A subset is a set that is contained within a set, for example {2, 4} is a subset of {2, 4, 6}. In general, a set can always be considered a subset of itself. The empty set, which has no elements, is always a subset of any set.
Now let's review the types of numbers we discussed in module 1.
The set of natural numbers is composed of the numbers we use to count objects.
The set of natural numbers is {1, 2, 3, 4, 5, ...}.
The set of whole numbers includes the set of natural numbers and the number 0.
The set of whole numbers is {0, 1, 2, 3, 4, 5, ...}.
The set of integers comprises the positive whole numbers, their opposites (negative numbers), and the number 0.
The set of integers is {...,–3, –2, –1, 0, 1, 2, 3, ...}.
The set of rational numbers is composed of numbers you have encountered previously—the positive and negative fractions discussed in module 1, section IV. Every element in this set of numbers can be represented as a quotient of integers. Notice that every integer is also a rational number because each integer can be expressed as a quotient of integers.
For example, the integer 5 is a rational number because 5 = 
. On a number line, rational numbers may be visualized as integers and many of the points between integers.
The set of rational numbers contains
any number that can be expressed as
,
where a and b are integers, and b
does not equal 0.
The number line also contains points that cannot be expressed as quotients of
integers. These numbers are called
irrational numbers because they cannot be represented as rational numbers.
For example,
and
are irrational numbers.
The set of irrational numbers contains any number that cannot be expressed as a rational number.
Both rational and irrational numbers can be written as decimal numbers. The decimal equivalent of a rational number will either terminate or repeat in a pattern. For example, upon dividing, we find that:
= 0.75 (decimal number terminates or ends)
= 0.6666... or 
(decimal number repeats in a pattern)
The decimal representation of an irrational number will neither terminate nor repeat. For example:
= 1.414213562... (non-repeating and non-terminating)
Combining the set of rational numbers with the set of irrational numbers gives the set of real numbers. One and only one point on a number line corresponds to each real number.
The set of real numbers is the set of all numbers, each of which corresponds to a point on a number line.
From the discussion above, we can note the following relationships:
Figure 2.1 shows the relationships among these sets.
Figure 2.1
Relationship among the Sets of Numbers
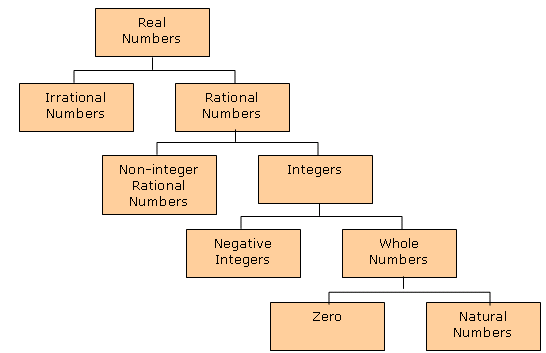
Note that "non-integer rational numbers" is a formal way of describing most fractions made up of integers. For example, 
is a non-integer rational number. In contrast, is considered an integer, because it can be written as 5.
In module 1, section II, you learned how to graph integers on a number line. Now, we extend the method to include graphing real numbers on a number line. As before, we label the number line with tick marks for the integer points.
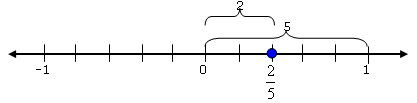
For example, to graph on a number line, divide the distance from 0 to 1 into 5 equal parts. Then start at 0 and count 2 parts to the right, as shown in figure 2.2 below.
Figure 2.2
Graphing a Real Number
In the next example, we will graph the irrational number
on a number line. First, use your calculator to find the decimal estimate of
as 1.414. Then, estimate the location of this number between 1 and 2, as shown
below. The location of 1.414 will be about
of the way between 1 and 1.5.
Figure 2.3
Graph of
We've already seen how to compare integers, decimals, and fractions. We demonstrated that for any two such numbers graphed on a number line, the number to the right is the greater number, and the number to the left is the smaller number. The symbols > and < are used to represent greater than and less than respectively. If two numbers are equal, we use the symbol =. We can compare two real numbers in the same way.
Example 1: Compare –0.74 and
.
Solution: First, write
as –0.75.
Then graph –0.74 and –0.75 on a number line.
Figure 2.4 shows the graph of –0.74 and –0.75 on the number line.
Figure 2.4
Graph of –0.74 and –0.75
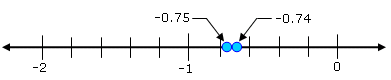
Because –0.74 is to the right of –0.75, we write –0.74 >
–.
| Example 2: | Compare
and 0.67. |
| Solution: | Because
can be written as 0.6666…, we can easily see it is smaller than 0.67,
and we write
< 0.67. |
In module 1, we discussed addition, subtraction, multiplication, and division of integers, fractions, and decimals, which comprise the set of rational numbers. Recall that the rational numbers are a subset of the real numbers. You will encounter arithmetic with irrational numbers later in your studies.
The same methods and rules for addition of rational numbers that were discussed in module 1 apply to the addition of real numbers, and are repeated below. Remember that when adding fractions, you must find the common denominator and add the equivalent fractions.
Adding Two Numbers with the Same Sign
| Step 1. | Add their absolute values. |
| Step 2. | Use their common sign as the sign of the sum. |
Adding Two Numbers with Different Signs
| Step 1. | Subtract the smaller absolute value from the larger absolute value. |
| Step 2. | Use the sign of the number with the larger absolute value as the sign of the sum. |
In module 1, section II, we defined the opposite of a number as the number that is the same distance from 0 on the number line but on the opposite side. Another term for opposite is additive inverse.
Additive Inverse (or Opposite) of a Number
Two numbers that are the same distance from 0 but lie on opposite sides of 0 are called additive inverses of each other.
For example, the additive inverse of 4 is –4 because each is 4 units away from 0, as shown on the number line below. Conversely, the additive inverse of –4 is 4.
Figure 2.5
Additive Inverse
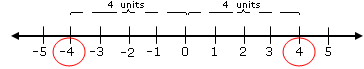
Another interesting characteristic of opposites is that the sum of a number and its opposite is 0, as you can see from the examples below.
10 + (–10) = 0
–3 + 3 = 0
+
= 0
In general, we can write the following:
The Sum of a Number and Its Inverse
The sum of a number a and its additive inverse –a is 0.
a + (–a) = 0
In module 1, section II, you learned how to subtract integers by adding the first number to the opposite, or additive inverse, of the second number. This rule also applies to the real numbers, and we formally state it below.
Subtracting Two Real Numbers
If a and b are real numbers, then a – b = a + (–b).
In module 1, section II, you learned that multiplying integers is similar to multiplying whole numbers, and you also learned how to determine the sign of the result. These rules are summarized below.
Multiplying Real Numbers
Multiplying Real Numbers: Helpful Hint
When multiplying more than two numbers, if we multiply:
What happens when one of the numbers being multiplied is 0? The result will be 0, regardless of the value of the other number.
Multiplying by Zero
If b is a real number, b · 0 = 0. Also, 0 · b = 0.
Just as every difference of two numbers a – b can be
written as the sum a + (–b), so, too, every quotient of two
numbers can be written as a product. For example, the quotient 6 ÷ 3 can be
written as
.
Recall that
is the
reciprocal, or multiplicative inverse, of 3. The product of a
number and its multiplicative inverse is 1.
Multiplicative Inverse (or Reciprocal) of a Number
Two numbers whose product is 1 are called multiplicative inverses (or reciprocals) of each other.
Notice that 0 has no multiplicative inverse, because 0 multiplied by any number is never 1; it is always 0.
We can now define division in terms of multiplication.
Division of Two Real Numbers
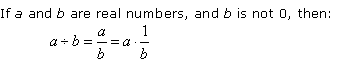
In other words, the quotient of two real numbers is the product of the first number and the multiplicative inverse, or reciprocal, of the second number.
Notice that the definition of the quotient of two real numbers does not allow for division by 0, because 0 does not have a multiplicative inverse. We say that division by 0 is not allowed or not defined, and that any number divided by 0 does not represent a real number. In other words, the denominator of a fraction can never be 0. On the other hand, the numerator of a fraction can be 0. For example,
In general, the quotient of 0 and any nonzero number is 0.
Zero as a Divisor or Dividend
The quotient of any nonzero real number and 0 is undefined.
The quotient of 0 and any real number except 0 is 0.
In this section, we give names to the properties of real numbers. Throughout this section, the variables a, b, and c represent real numbers.
Before we begin, let's define what we mean by "equivalent expressions."
Equivalent Expressions
Two algebraic expressions are equivalent if they evaluate to the same real number regardless of the value of the variables.
For example, the expressions a + 2b and a + b + b are equivalent because regardless of what values we substitute for a and b in each expression, both expressions will evaluate to the same number. Try substituting pairs of numbers into these two expressions to prove this for yourself.
We use the equal sign to indicate that two expressions are equivalent. For example, we write:
a + 2b = a + b + b
In this section, we will use the concept of equivalence as we define the properties of real numbers.
Let's begin by discussing the identity properties.
The number 0 is called the identity for addition because when 0 is added to any real number, the number remains unchanged.
Similarly, the number 1 is called the identity for multiplication because when a real number is multiplied by 1, the number is not changed.
Identities for Addition and Multiplication
0 is the identity element for addition.
a + 0 = a and 0 + a = a
1 is the identity element for multiplication.
a · 1 = a and 1 · a = a
We know that the order does not matter when adding numbers. For example, 7 + 5 is equivalent to 5 + 7. This property is given a special name: the commutative property of addition. We also know that order does not matter when multiplying numbers; this property is called the commutative property of multiplication.
Commutative Properties
| Addition: |
a + b = b + a |
| Multiplication: | a · b = b · a |
These properties state that the order in which any two real numbers, a and b, are added or the order in which they are multiplied does not matter, as the result will be an equivalent expression.
Let's now discuss grouping numbers. We know that when we add three numbers, the way in which they are grouped (or associated) does not matter, as the result will be an equivalent expression. In other words:
2 + (3 + 4)
is equivalent to
(2 + 3) + 4
This property is called the associative property of addition.
Similarly, we know that changing the grouping of numbers when multiplying does not change the product. For example, 2 · (3 · 4) is equivalent to (2 · 3) · 4. This is called the associative property of multiplication.
Associative Properties
| Addition: |
(a + b) + c = a
+ (b + c) |
| Multiplication: | (a · b) · c = a
· (b ·
c) |
The associative properties state that the way in which three numbers, a, b, and c, are grouped does not matter, as the result will be an equivalent expression.
The distributive property of multiplication over addition is used repeatedly throughout algebra. It is useful because it allows us to write a product as a sum, or a sum as a product.
We know that:
7(2 + 4) = 7(6) = 42
Compare the statement above with the one below:
7(2) + 7(4) = 14 + 28 = 42
Because both original expressions equal 42, they must be equivalent expressions. In other words:
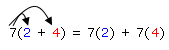
This is an example of the distributive property. The product on the left side of the equal sign is equivalent to the sum on the right side. We can think of the 7 as being distributed over each number inside the parentheses.
Distributive Property of Multiplication over Addition
Because multiplication is commutative, this property can also be written as:
(b + c)a = ba + ca
The distributive property can be extended to more than two numbers inside the parentheses, as shown in the example below:
3(x + y + z) = 3(x) + 3(y) + 3(z)
= 3x + 3y + 3z
Finally, because we have defined subtraction in terms of addition, the distributive property also applies to subtraction.
a(b – c) = ab – ac
Now let's look at some examples using the distributive law.
| Examples: | Use the distributive property to write equivalent expressions without parenthesis. Simplify your answers if possible. |
| a. 2(3x + 5y) = 2(3x) +
2(5y) = 6x + 10y |
Apply the distributive property. Multiply. |
| b. –5(–3 + 2z) = –5(–3) + (–5)(2z) = 15 + (–10z) = 15 – 10z |
Apply the distributive property. Multiply. Simplify. |
|
c. –(3 + x –w) = –1(3 + x
– w) = (–1)(3) + (–1)(x) – (–1)(w) = –3 – x + w |
Write –( ) as –1( ). Apply the distributive property. Multiply and simplify. |
After completing this section, you should be able to:
Just as we can add, subtract, multiply, and divide real numbers, we can also add, subtract, multiply, and divide algebraic expressions. Previously, we evaluated algebraic expressions such as 4x, x + 3, and x + 26 for particular values of the variables. In this section, we explore working with algebraic expressions without evaluating them for particular values.
Before we can explain how to combine like terms, we must define what we mean by a term. In an expression such as x + 3, each item that is added is called a term. Thus, x is a term and 3 is a term, and therefore the expression has two terms. Expressions can have any number of terms, as seen in the two expressions below.
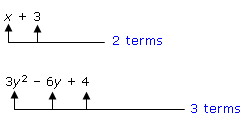
A term that has only a number is called a constant term or constant. A term that contains a variable is called a variable term. The number factor of a variable term is called the numerical coefficient, or coefficient. If the coefficient is 1, it is usually not written.
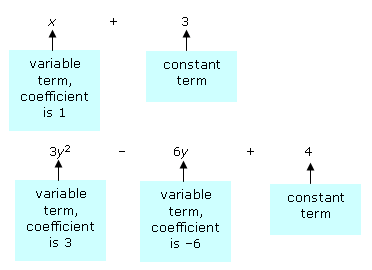
Terms that contain the same variables raised to the same exponents are called like terms. For example, 3x and 7x are like terms, as are –6y2 and 2y2. However, 3x and 3y are not like terms, nor are 2y and 2y2. Why? Such terms are called unlike terms. Only like terms can be added or subtracted. We say that we are combining like terms when we add or subtract like terms.
To combine like terms, we make use of the distributive property from the previous section. Recall that we can write the distributive property as:
(a + b)c = ab + ac
If we reverse sides, we get:
ab + ac = (a + b)c
By the distributive property then:
7x + 2x = (7 + 2)x = 9x
We have combined like terms, and the expression 7x + 2x is equivalent to 9x.
Let's look at some examples where we combine like terms.
Examples: Simplify by combining like terms.
|
a. 3x + 2x |
= (3 + 2)x = 5x |
Apply the distributive property. Add. |
|
b. y – 7y |
= 1y – 7y = (1 – 7)y = –6y |
Write the coefficient of 1. Apply the distributive property. Subtract. |
|
c. 3x2 + 5x2 |
= (3 + 5)x2 – 2 = 8x2 – 2 |
Apply the distributive property. Add. |
The commutative and associative properties can also help us simplify expressions, as shown in the example below.
Example: Simplify 4x + 2 – 5x + 3.
Solution:
| 4x + 2 – 5x + 3 | |
= 4x + 2 + (–5x) + 3 |
Rewrite as addition. |
= 4x + (–5x) + 2 + 3 |
Use the commutative property to rearrange terms. |
= [4x + (–5x)] + [2 + 3] |
Use the associative property to group like terms. |
= –1x + 5 |
Add. |
= –x + 5 |
Simplify. |
We also can use properties of numbers to multiply expressions such as 3(2x). By the associative property of multiplication, we can write the product 3(2x) as (3 · 2)x, which simplifies to 6x.
Example: Multiply –2(4x).
Solution:
|
–2(4x) = (–2 · 4)x |
Apply the associative property of multiplication. Multiply. |
Previously, we used the distributive property to write equivalent expressions without parentheses. Next, we will simplify expressions by first using the distributive property to multiply, and then we will combine any like terms.
Example 1: Simplify 2(3 + x) – 15.
Solution:
| 2(3 + x) – 15 = 2 · 3 + 2 · x + (–15) = 6 + 2x + (–15) = 2x + (–9) = 2x – 9 |
Apply the distributive property. Multiply. Combine like terms. Simplify. |
Example 2: Simplify –2(x – 5) + 4(2x + 2).
Solution:
–2(x – 5) + 4(2x + 2) = –2 · x
+ (–2)(–5) + 4 · 2x + 4 · 2
= –2x + 10 + 8x + 8
= 6x + 18
We have used the distributive property to write a product as a sum. It is also possible to use the distributive property in reverse to write a sum as a product. Before we do this, we must discuss the greatest common factor.
In module 1, section III, we defined factoring a number as expressing that number as a product of other numbers. Each of these numbers is called a factor of the original number. For example, we can factor 30 as 2 · 3 · 5, where 2, 3, and 5 are called factors of 30.
The product 2 · 3 · 5 is called a factorization of 30, and because each of the factors is prime, 2 · 3 · 5 is the prime factorization of 30. Note that there is only one prime factorization of any number.
The greatest common factor (GCF) of a list of integers is the largest integer that is a factor of all the integers in the list. For example, the GCF of 30 and 18 is 6, because 6 is the largest integer that is a factor of both 30 and 18. If you cannot find the GCF by inspection, you can find it by following the steps below.
To Find the GCF of a List of Integers
| Step 1. | Find the prime factorization of each number in the list. |
| Step 2. | Identify the common prime factors. |
| Step 3. | The product of all common prime factors found in Step 2 is the GCF. If there are no common prime factors, the greatest common factor is 1. |
Let's look at some examples showing how to find the GCF of a number.
Example: Find the GCF of 12 and 20.
Solution:
| Step 1. | Find the prime factorization of each number 12 = 2 · 2 · 3 |
Step 2. |
Identify the common prime factors.
|
Step 3. |
The GCF is 2 · 2 = 4. |
To find the GCF of a list of variables that are raised to powers, such as x2 and x5, first write each term as a product. Then, use the steps given above to find the GCF.
Example 1: Find the GCF of x2 and x5.
Solution:
Step 1. |
Find the prime factorization of each term.
x2 = x · x |
Step 2. |
Identify the common prime factors.
|
Step 3. |
The GCF is x · x = x2 |
You can avoid going through these steps if you note that that the GCF is simply the variable raised to the smallest exponent.
Finding the GCF of a List of Terms
The GCF of a list of variables raised to powers is the variable raised to the smallest exponent in the list.
The GCF of a list of terms is the product of all common factors.
Example 2: Find the GCF of 4x3, 12x, and 10x5.
Solution:
The GCF of 4, 12, and 10 is 2.
The GCF of x3, x1, and x5
is x1.
Thus, the GCF of 4x3, 12x, and 10x5
is 2x1
or 2x.
Next, we practice factoring an algebraic expression by factoring out the GCF from its terms. Recall that the distributive property states that a(b + c) = ab + ac.
In reverse, we get ab + ac = a(b + c). We will use this form of the distributive property to factor out the GCF from an expression.
Example 1: Factor 8x + 4.
Solution:
The GCF of 8x and 4 is 4. 8x + 4 = 4 · 2x + 4 · 1 |
Write each term as the product of the GCF and the remaining factor. |
| = 4(2x + 1) | Apply the distributive property. Don't forget to write down the term of 1. |
Example 2: Factor 7x3 – 14x2.
Solution:
| The GCF of 7x3 and 14x2 is 7x2 | Apply the distributive property. |
| 7x3 – 14x2 = 7x2 · x1 + 7x2 · 2 | |
| = 7x2(x + 2) |
Remember that you can check your answer by multiplying, as we have done below.
7x2(x + 2) = 7x2
· x1 + 7x · 2
= 7x3 – 14x2
Example 3: Factor –2a + 20b – 4b2.
Solution:
| When the coefficient of the first term is
negative, we usually factor out a negative GCF. The GCF of –2a, 20b,
and –4b2 is –2. |
|
| –2a
+ 20b – 4b2 = –2
·
a + (–2)(–10b) + (–2)(2b2) |
|
