Module 3: Real Numbers

Topics

1. Algebraic Expressions and Sets of Numbers
2. Operations on Real Numbers
3. Properties of Real Numbers

I. Algebraic Expressions and Sets of Numbers

After completing this section, you should be able to:

• identify algebraic expressions
• identify natural numbers, whole numbers, integers, rational real numbers, and irrational real numbers
• find the absolute value of a number
• write phrases as algebraic expressions

A. Algebraic Expressions

Previously, you learned that letters that represent numbers are called variables. An algebraic expression is formed by numbers and variables connected by the operations of addition, subtraction, multiplication, and division, or by numbers or variables raised to a power. The following are examples of algebraic expressions, or more simply, expressions.

• 3x + 5

• 2x³ –3x + 1

• 

B. Word Statements and Equivalent Math Statements

When we solve problems, we often must translate a phrase into an algebraic expression. The following table lists key words that will help you translate the operations of addition, subtraction, multiplication, and division.

Example 1:

Translate each phrase into an algebraic expression. Use the variable x to represent each unknown number.

C. Sets

Set Notation

Before we can discuss the common sets of numbers—including the set of real numbers—we must introduce set notation. A set is a collection of objects. For example, we can talk about the set of all toys in a box or the set of numbers in your social security number.

The members of a set are called its elements. When the elements of a set are given in a list, we enclose the elements in braces. This form is sometimes referred to as the roster form for a set. For example, the set of positive whole numbers less than 3 can be written as:

{1, 2}

A set that contains no elements is called the empty set and is written as { } or ∅.

A set can also be written in a notation that describes the members of a set but does not list them. This form is sometimes referred to as set builder notation. Using the example above, we can write the set as:

{x | x is a positive number less than 3}

This statement is read:

"The set of all x such that x is a positive number less than 3."

Note that the symbol | is read "such that."

Here are some examples to help you become familiar with this notation. Read each expression aloud; then move your mouse over "read this aloud" to see what you should have said. Then try to determine the numbers in each set before you look at our answer.

• {x | x is an even whole number between 1 and 5}            read this aloud   Set =
• {y | an odd whole number between 2 and 6}                   read this aloud   Set =
• {w | w is a whole number greater than 7 and less than 5} read this aloud   Set =

Study the examples above to be sure you understand why the numbers in each set are correct, then try the examples below yourself.

Example 2: List the elements in each set.

1. {x | x is a whole number between 1 and 6}      Solution

2. {x | x is a whole number greater than 100}      Solution

We could not list the entire solution to the second problem. To indicate that the list continues in the same pattern, we use the symbol … , called an ellipsis.

Elements of a Set

The symbol ∈ is used to denote that an element is in a particular set. The symbol is read as "is an element of" or "is a member of." For example, 3 is an element of the set {1, 2, 3, 4}, and we write this as:

3 ∈ {1, 2, 3, 4}

The symbol ∉ is used to denote that an item is not an element of a set. Again referring to the set {1, 2, 3, 4}, we can write:

5 ∉ {1, 2, 3, 4}

Subsets

When all the elements of one set are also elements of another set, we say that the first set is a subset of the second set. For example, the set {1, 2} is a subset of the set {0, 1, 2, 3, 4}. We use the symbol ⊆ to denote "is a subset of." Thus,

{1, 2} ⊆  {0, 1, 2, 3, 4}

Let's look at one more example that clarifies what a subset is.

Let:

set A = {4, 5, 6}
set B = {1, 2, 3, 4, 5, 6}
set C = {5, 6, 7}

Then A ⊆  B. Click on the Play button in figure 3.1 to see this example demonstrated.

Figure 3.1
A Subset Example

On the other hand, C is not a subset of B. Click on the Play button in figure 1.2 to see this example demonstrated.

Figure 3.2
A Non-Subset Example

D. Sets of Numbers

Some common sets of numbers are shown in the following table.

We can show the relationships among these sets of numbers in the following diagram.

Figure 3.3
Relationships among the Sets of Numbers

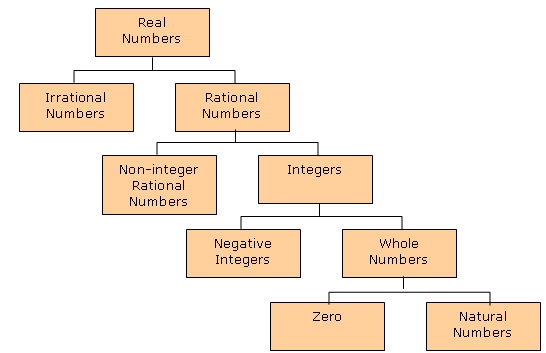
Now that you have seen the relationships among the various sets of numbers, try these examples.

Example 3:

List the elements of the set {x | x is a natural number less than 5}    Solution

Example 4:

List the elements of the set {3, 0, , , , –134} that are also elements of the set of whole numbers.    Solution

Example 5: Determine whether the following statements are true or false.

E. Absolute Value

We can use the number line to visualize the distance from zero, which leads to the concept of absolute value. The absolute value of a real number a, written as |a|, is the distance between a and 0 on the number line. Because distance is always positive or zero, |a| is always positive or 0. The figure below depicts this concept.

Figure 3.4
Absolute Value

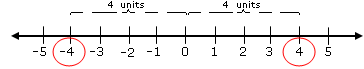
Using the number line, we see that:

|4| = 4

and also

|–4| = 4

because both 4 and –4 are a distance of 4 units from 0. We can also define the absolute value of a real number in this way:

|a| = +a if a is 0 or a positive number
|a| = –a if a is a negative number

Example 6: Find each absolute value.

1. |–5|      Solution

2. –|–8|    Solution

II. Operations on Real Numbers

After completing this section, you should be able to:

• add, subtract, multiply, and divide real numbers
• simplify expressions containing exponents
• use the order of operations
• evaluate algebraic expressions

When solving problems, we often must perform arithmetic operations on real numbers. In this section, we will discuss the operations of addition, subtraction, multiplication, and division, and also learn how to use exponential notation with real numbers.

A. Adding Real Numbers

Example 1:  Add.

1. –3 + (–11)

   Solution:  The two numbers have the same sign (negative), so we add their absolute values (3 + 11) and use that sign.  –3 + (–11) = –(3 + 11) = –14

2. 3 + (–7)

   Solution:  3 + (–7) = –4

3. –10 + 15

   Solution:  –10 + 15 = 5

B. Subtracting Real Numbers

In other words, to subtract a real number, just add the opposite number.

Example 2:  Subtract.

1. 2 – 8

   Solution:  2 – 8 = 2 + (–8) = –6

2. –8 – (–1)

   Solution:  –8 – (–1) = –8 + (+1) = –7

3. –11 – 5

   Solution:  –11 – 5 = –11 + (–5) = –16

C. Multiplying Real Numbers

Also, recall that the product of zero and any real number is 0.

In general, if we are multiplying more than two real numbers, the sign of the product depends on the number of negative numbers being multiplied.

Note that the number of positive factors has no effect on the sign of the product.

Example 3:  Multiply.

1. (–8)(–1)

   Solution:

   The product of two numbers with the same sign is positive. Or, you can think of this as being the product of an even number (two) of negative factors, so the product is positive. Therefore:

   (–8)(–1) = +8 or 8

2. 3(–3)

   Solution:

   The product of two numbers with different signs is negative. Or, you can think of this as being the product of an odd number (one) of negative factors. Therefore:

   3(–3) = –9

3. 0(11)

   Solution: The product of any real number and 0 is 0.

   0(11) = 0

4. (–2)(–1)(–3)

   Solution: Because there is an odd number (three) of negative factors, the product is negative.

   (–2)(–1)(–3) = –6

D. Dividing Real Numbers

To find the solution to a ÷ b, we can divide by b or multiply by 1/b. The nonzero numbers b and 1/b are reciprocals of each other. Notice that b must be a nonzero number because division is not defined for a zero divisor.

Example 4: Divide.

1. 

   Solution: Because the signs are different, the quotient is negative.

   = –5

2. 

   Solution:

   

3. 

   Solution:

   is undefined.

Notice that the sign rules for division are not affected by the position of the negative sign in a fraction. For example:

Thus, we can say that:

In general, if a and b are real numbers and b ≠ 0, then:

E. Exponents

An exponent is a shorthand notation for repeated multiplication. When the same number is a factor several times, we can use an exponent. For example, in the product 2 · 2 · 2 · 2 · 2, the number 2 is a factor 5 times.

Using an exponent, this product can be written as:

Thus,

2 · 2 · 2 · 2 · 2 = 2⁵

This is called exponential notation. The exponent, 5, indicates how many times the base, 2, is a factor.

When the base is negative, be sure to put parentheses around the base. For example:

(–2)⁴ = (–2) · (–2) · (–2) · (–2) = 16

If we did not use parentheses around the base, we would get a different answer:

–2⁴ = –(2) · (2) · (2) · (2) = –16

Watch this animation showing how to evaluate exponential expressions.

F. Order of Operations

Expressions containing more than one operation are written to follow a particular agreed-upon order of operations. For example, when we write 3 + 2 · 10, we mean to multiply first, and then add, as shown in Example 5, below.

Example 5: Simplify.

1. 3 + 2 · 10

   Solution: First multiply, then add.

   3 + 2 · 10 = 3 + 20 = 23

2. 2(1 – 4)²

   Solution: The interactive diagram below will step through the solution.

    

3. 

   Solution: The interactive diagram below will step through the solution.

G. Algebraic Expressions

Evaluating Algebraic Expressions

To find the value of an algebraic expression, we replace the variables with the given values and evaluate the resulting numerical expression. This process is called evaluating an expression.

Watch this animation showing how to evaluate expressions.

Now try to work out these examples yourself, then click on Solution to see our answers.

Example 6: Evaluate each expression when x = 2, y = –1, and z = –3.

1.  3x + y      Solution

2.  z – y        Solution

3.  z²           Solution

4.       Solution

III. Properties of Real Numbers

After completing this section, you should be able to:

• use operation and inequality symbols to write mathematical sentences
• identify identity numbers and inverses
• identify and use the commutative, associative, and distributive properties
• write and simplify algebraic expressions

A. Equality

Earlier in this module, we used the symbol = to mean "is equal to." The following words and phrases also imply equality:

• equals
• is/was
• represents
• is the same as
• gives
• yields
• amounts to

If we wish to use symbols to indicate that two numbers are not equal, we use the symbol ≠, which means "is not equal to."

Example 1: Write each sentence using mathematical symbols.

1. The sum of x and 5 is 20.

   Solution:    x + 5 = 20

2. If x is subtracted from 8, the difference is the same as twice x.

   Solution:    x – 8 = 2x

3. 11 is not equal to z

   Solution:    11 ≠ z

To compare two numbers, we use the symbols < or > to mean "is less than" or "is greater than," respectively. If we graph two numbers on a number line, we say that:

• a < b if the number a lies to the left of b on the number line.

• a > b if the number a lies to the right of b on the number line.

In addition to < and >, we have the inequality symbols ≤ and ≥.

• The symbol ≤ means "is less than or equal to."

• The symbol ≥ means "is greater than or equal to."

Example 2: Write each sentence using mathematical symbols.

1. The sum of 5 and y is greater than or equal to 7.

   Solution: 5 + y ≥ 7

2. 20 is less than the difference of 5 and twice x.

   Solution: 20 < 5 – 2x

B. Identities and Inverses

When the number 0 is added to any real number, the real number remains unchanged. We call 0 the additive identity. We can express this rule as:

a + 0 = a

Similarly, when the number 1 is multiplied by any real number, the real number remains unchanged. We call 1 the multiplicative identity. We can express this rule as:

a · 1 = a

The sum of a number a and its opposite (–a) is always 0. We call the opposite the additive inverse.

Similarly, the product of a nonzero number a and its reciprocal 1/a is always 1, and we call the reciprocal the multiplicative inverse.

Example 3: Find the additive inverse, or opposite, of each number.

1. 8

   Solution: The opposite of 8 is –8.

2. 

   Solution: The opposite of .

Example 4: Find the multiplicative inverse, or reciprocal, of each number.

1. 8

   Solution: The reciprocal of 8 is .

2. 

   Solution: The reciprocal of is 5.

C. Commutative Property

All real numbers have certain properties that allow us to write equivalent expressions. The commutative properties state that the order in which two real numbers are added or multiplied does not affect their sum or product.

Example 5: Use the commutative property of addition or multiplication to write equivalent expressions.

1. 7x + 5

   Solution: The interactive diagram below will step through the solution.

    

2. r · x

   Solution: Using the commutative property of multiplication,  r · x = x · r

D. Associative Property

The associative properties state that regrouping numbers that are added or multiplied does not affect their sum or product.

Example 6: Use an associative property to write equivalent expressions.

1. (7x + 5) + y

   Solution: The interactive diagram below will step through the solution.

    

2. x · (4y)

   Solution: Using the associative property of multiplication,

   x · (4y) = (x · 4) · y

E. Distributive Property

The distributive property states that multiplication distributes over addition.

Example 7: Use the distributive property to multiply.

1. 3(2x + y)

   Solution:    3(2x + y) = 3 · 2x + 3 · y = 6x + 3y

2. –(3x – 1)

   Solution:    Recall that –(3x – 1) is equivalent to –1(3x – 1).

   –1(3x – 1) = –1(3x) + (–1)(–1) = –3x + 1

F. Simplifying Algebraic Expressions

To simplify algebraic expressions, we use the commutative, associative, and distributive properties to rearrange, regroup, remove grouping symbols, and combine like terms.

Example 8: Simplify each expression.

1. 3x + 4 – 5x

   Solution:

   3x + 4 – 5x	=	3x – 5x + 4	Applied the commutative property.
   	=	(3x – 5x) + 4	Applied the associative property.
   	=	(3 – 5)x + 4	Applied the distributive property.
   	=	–2x + 4	Simplified.

   
   

2. (3x + 4) –(6x –1)

   Solution:

   (3x + 4) – (6x – 1)	=	3x + 4 – 6x + 1	Applied the distributive property.
   	=	3x – 6x + 4 + 1	Applied the commutative property.
   	=	(3x – 6x) + (4 + 1)	Applied the associative property.
   	=	–3x + 5	Combined like terms.

Return to top of page