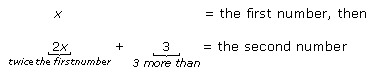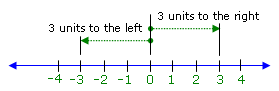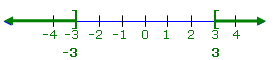Module 4: Problem Solving with Equations and Inequalities
Topics
- Linear Equations in One Variable
- An Introduction to Problem Solving
- Linear Inequalities
- Compound Inequalities
- Absolute Value Equations
- Absolute Value Inequalities
After completing this section, you should be able to:
- solve linear equations using properties of equality
- solve linear equations that can be simplified by combining like terms
- solve linear equations containing fractions
- identify equations that are identities and those that have no solution
A. Linear Equations in One Variable
A linear equation in one variable is a statement that two
expressions are equal. For example,
3x + 5 = 8
is a linear equation in one variable. If the variable in the equation is
replaced by a number and the resulting equation, or statement, is true, that
number is called a solution of the equation.
For example, the number 1 is a solution of the equation 3x + 5 = 8 because:
3(1) + 5 = 8 is a true statement
But the number 2 is not a solution of this equation because:
3(2) + 5 = 8 is not a true statement
The solution set of an equation is the set of solutions of
the equation. In the example above, the solution set is {1}.
To solve an equation we must find the solution set of the equation. Equations
with the same solution set are called equivalent equations. For example:
are all equivalent equations because they all have the same solution set of {1}.
To solve an equation for a variable, we start with the given equation and
write a series of simpler equivalent equations until we obtain an equation of
the form:
x = number
To accomplish this, we use two important properties of equality, the addition
and multiplication properties.
B. Addition and Multiplication Properties of Equality
The Addition and Multiplication Properties of Equality
If a, b, and c are real numbers, then:
a = b and a + c
= b + c are equivalent equations
a = b and ac = bc are
equivalent equations
In other words, the addition property of equality guarantees that when
the same number is added to both sides of an equation, the result will be an
equivalent equation.
Similarly, the multiplication property of equality guarantees that when the
same number multiplies both sides of an equation, the result is an
equivalent equation. Because subtraction can be defined in terms of addition and
division can be defined in terms of multiplication, we can also subtract the
same number from both sides of an equation, or divide both sides of an equation by the same
nonzero number.
Example 1: |
Solve for x: 2x + 5 = 9 |
| |
|
| Solution: |
First, use the addition property of equality to subtract 5 from both sides.
| 2x + 5 |
= |
9 |
Original equation. |
| 2x + 5 –5 |
= |
9
–5 |
Subtracted 5 from both
sides. |
| 2x |
= |
4 |
Combined like terms. |
Now, use the multiplication property of equality to divide both sides by 2 to isolate the
variable.
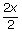 |
= |
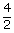 |
Divided both sides by
2. |
| x |
= |
2 |
Simplified. |
|
| Check: |
Check that 2 is the solution by substituting 2 for x in the original
equation.
| 2x + 5 |
= |
9 |
Original equation. |
| 2(2) + 5 |
= |
9 |
Replaced x with
2. |
| 4 + 5 |
= |
9 |
Multiplied. |
| 9 |
= |
9 |
True. |
|
C. Solving Linear Equations in One Variable
Often, before we can begin using the properties of equality, we must simplify
each side of an equation by removing grouping symbols and combining like terms.
Example 2: |
Solve for x: 3(x + 2) = 11 –2(2 –x) |
| |
|
| Solution: |
First, use the distributive property to remove parentheses, and then combine like terms on each
side of the equation.
| 3(x + 2) |
= |
11 – 2(2 – x) |
Original equation. |
| 3x + 6 |
= |
11 – 4 + 2x |
Used the distributive property. |
| 3x + 6 |
= |
7 + 2x |
Combined like terms. |
Now, use the properties of equality to solve the equation.
| 3x + 6 – 6 |
= |
7 + 2x – 6 |
Added –6 to both sides. |
| 3x |
= |
1 + 2x |
Combined like terms. |
| 3x – 2x |
= |
1 + 2x – 2x |
Added –2x to both sides. |
| x |
= |
1 |
Combined like terms. |
|
If an equation contains fractions, we first clear the equation of fractions by multiplying both
sides of the equation by the least common denominator (LCD) of all the fractions in the equation.
As a general guideline, the following steps may be used to solve a linear
equation in one variable.
Solving a Linear Equation in One Variable
| Step 1. |
Clear the equation of fractions by multiplying each side of the equation by the least common
denominator. |
| Step 2. |
Use the distributive property to remove grouping symbols such as parentheses. |
| Step 3. |
Combine like terms on each side of the equation. |
| Step 4. |
Use the addition property of equality to rewrite the equation as an equivalent equation with
variable terms on one side and numbers on the other side. |
| Step 5. |
Use the multiplication property of equality to isolate the variable. |
| Step 6. |
Check the proposed solution in the original equation. |
Lastly, we will look at linear equations that either have no solution or have more than one
solution. These equations are called contradictions or identities, respectively.
- contradiction—an equation in one variable that has no
solution
- identity—an equation in one variable that has all numbers
as solutions
Example 4: |
Solve for x: 3x + 5 = 3(x + 2) |
| |
|
| Solution: |
First, use the distributive property to simplify.
| 3x + 5 |
= |
3(x + 2) |
Original equation. |
| 3x + 5 |
= |
3x + 6 |
Distributed 3. |
| 3x + 5 – 3x |
= |
3x + 6 – 3x |
Subtracted 3x from both sides. |
| 5 |
= |
6 |
Combined like terms. |
|
|
The equation 5 = 6 is a false statement no matter what value the variable x might have.
Thus, the original equation has no solution. Its solution set is written either as:
{ } or Ø
Example 5: |
Solve for x: 6x – 4 = 2 + 6(x – 1) |
| |
|
| Solution: |
First, use the distributive property to simplify.
| 6x – 4 |
= |
2 + 6(x – 1) |
Original equation. |
| 6x – 4 |
= |
2 + 6x – 6 |
Distributed 6. |
| 6x – 4 |
= |
6x – 4 |
Combined like terms. |
| 6x – 4 + 4 |
= |
6x – 4 + 4 |
Added 4 to both sides. |
| 6x |
= |
6x |
Combined like terms. |
| 6x –6x |
= |
6x –6x |
Subtracted 6x from both sides. |
|
= |
|
Combined like terms. |
|
|
Because 0 = 0 is a true statement for every value of x, all real
numbers are solutions. The solution set is the set of all real numbers, which
can be written:
{x | x is a real number}
After completing this section, you should be able to:
- write algebraic expressions that can be simplified
- apply the steps for problem solving
- solve a formula for a specified variable
- use formulas to solve problems
A. Writing Algebraic Expressions from Word Statements
In module 1, we practiced translating phrases into algebraic expressions. In
this section, we will practice writing algebraic expressions and then
simplifying them.
The first example involves consecutive integers. Consecutive integers
are integers that follow one another in order. For example, 6, 7, and 8 are
three consecutive integers. We will also study consecutive even integers and
consecutive odd integers. For example, 10, 12, and 14 are consecutive even
integers, whereas 7, 9, and 11 are consecutive odd integers.
Using variables, here's how we represent consecutive integers:
| Consecutive integers |
x, x + 1, x + 2, … |
| Consecutive even integers |
x, x + 2, x + 4, … |
| Consecutive odd integers |
x, x + 2, x + 4, … |
You may wonder why we add 2 to the first consecutive odd integer to get the second consecutive
odd integer. An example will make the reason clear. Consider the odd integer 7. The next odd
integer is 9, which is 2 units more than the first integer. Thus, if the first consecutive odd
integer is represented by x, the second will be 2 units more, or x + 2.
Example 1: |
Write the following as an algebraic expression, then simplify.
the sum of three consecutive integers, if x is the
first consecutive integer |
| |
|
| Solution: |
If we represent the first integer by x, the next two consecutive integers can
be represented by x + 1 and x + 2. Therefore, the sum can be written as:
x + (x + 1) + (x + 2)
Simplifying, we obtain:
x + (x + 1) + (x + 2) = x +
x + 1 + x + 2
=
3x + 3
|
Example 2: |
Write the following as an algebraic expression, then simplify.
the perimeter of a triangle with sides of length x, 5x,
and 6x – 3 |
| |
|
| Solution: |
The perimeter of a triangle is the sum of the lengths of the sides.
x + 5x + (6x – 3)
Simplifying, we obtain:
x + 5x + (6x – 3) = x + 5x
+ 6x – 3
=
12x – 3
|
B. General Strategy for Problem Solving
The following problem-solving strategy will be used throughout this course.
General Strategy for Problem Solving
| Step 1. |
UNDERSTAND the problem. During this step, become comfortable with the problem. Some ways of
doing so are as follows:
- Read and reread the problem.
- Choose a variable to represent the unknown.
- Construct a drawing, if possible.
- Propose a solution and check it. Pay careful attention to how you check your proposed solution,
which will help when writing an equation to model the problem.
|
| Step 2. |
TRANSLATE the problem into an equation. |
| Step 3. |
SOLVE the equation. |
| Step 4. |
INTERPRET the results. Check the proposed solution in the stated problem and state your
conclusion. |
Now let's see how to apply these rules.
 |
Watch this animation explaining . |
| |
|
| Example 3: |
Find two numbers such that the second number is 3 more than twice the first number and the
sum of the two numbers is 72.
|
| |
|
| Solution: |
1. UNDERSTAND the problem.
First let's read and reread the problem and then propose a solution. For example, let's guess
that the first number is 25.
Then the second number is 3 more than twice 25, or 3 + 2(25) = 53.
The sum of 25 and 53 is 78, which is not the required sum, but we have gained some valuable
information about the problem. First, we know that the first number is less than 25 because our
guess led to a sum larger than the required sum. Also, we have gained some information as to how
to model the problem with an equation.
Helpful Hint
The purpose of proposing a solution is not to guess the correct answer, but to gain
confidence, to help understand the problem, and determine how to model it.
Next, let's assign a variable and use this variable to represent any other unknown quantities.
If we let:
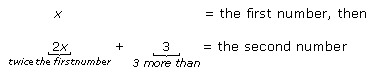
2. TRANSLATE the problem into an equation.
To do this, we use the fact that the sum of the numbers is 72. First let's write this
relationship in words and then translate into an equation.
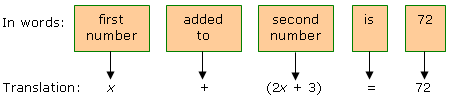
3. SOLVE the equation.
| x + (2x
+ 3) |
= |
72 |
Original equation. |
| x + 2x + 3 |
= |
72 |
Removed parentheses. |
| 3x + 3 |
= |
72 |
Combined like terms. |
| 3x |
= |
69 |
Subtracted 3 from both sides. |
| x |
= |
23 |
Divided both sides by 3. |
4. INTERPRET the results.
Here, we check our work and state the solution. The second number is
represented by 2x + 3. Therefore, because the first number is 23, the second
number is 49, calculated below:
2x + 3 = 2(23) + 3 = 49
Check your work: Is the second number 3 more than twice the
first number? Yes, because 3 more than twice 23 is 3 + 46, or 49. The sum of the
two numbers, 23 + 49 = 72, is the required sum.
State the solution: The two numbers are 23 and 49.
|
| |
|
| Example 4: |
Suppose that a computer store just announced an 8% decrease in the price of a
particular computer. If the computer sells for $2,162 after the decrease, find the
original price of the computer.
|
| |
|
Solution: |
1. UNDERSTAND the problem.
Read and reread the problem. Recall that a percent decrease means a percent of the original
price. Let's guess that the original price of the computer is $2,500.
The amount of decrease is then 8% of $2,500:
(0.08)($2,500) = $200
Therefore, the new price of the computer is the original price minus the decrease:
$2,500 – $200 = $2,300
Our guess is incorrect, but we now have an idea of how to model this problem. In our model,
we will:
let x = the original price of the computer
2. TRANSLATE the problem into an equation. To do this, we use the fact that the sum of the
numbers is 72. First let's write this relationship in words and then translate to an
equation.
In words:
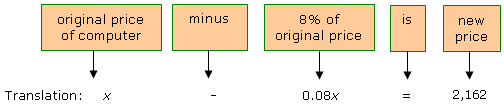
3. SOLVE the equation.
| x – 0.08x |
= |
2,162 |
Original equation.
Remember that x is the same as 1x. |
| 0.92x |
= |
2,162 |
Combined like terms. |
| x |
= |
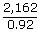 |
Divided both sides by 0.92. |
| x |
= |
2,350 |
Simplified. |
4. INTERPRET the results. Here, we check our work and state the solution.
Check your work: If the original price of the computer was
$2,350, the new price is $2,162, as shown in the following calculation:
$2,350 – (0.08)($2,350) = $2,350 – $188 = $2,162
State the solution: The original price of the computer was $2,350.
|
We've seen some problem-solving approaches to solving linear equations. Now let's look
at problem solving using formulas.
C. Formulas and Problem Solving
A formula is an equation that describes a known relationship
among quantities such as time, area, or volume. Some examples of formulas are
given below.
| Formula |
Meaning |
I = PRT
A = lw
d = rt
V = lwh |
interest = principal · rate · time
area of a rectangle = length · width
distance = rate · time
volume of a rectangular solid = length · width · height |
Let's consider the last formula. Note that this formula is solved for the variable
V, that is, V is by itself on one side of the equation and there are
no V's on the other side. Sometimes, however, it is useful to solve a formula for
different variable in the equation, that is, we want to have a different variable isolated on one
side of the equation.
Example 5: Solve V = lwh for h.
The following steps may be used to solve formulas or equations for a specified variable.
Solving Equations for a Specified Variable
| Step 1. |
Clear the equation of fractions by multiplying each side of the equation by the least common
denominator. |
| Step 2. |
Use the distributive property to remove grouping symbols such as parentheses. |
| Step 3. |
Combine like terms on each side of the equation. |
| Step 4. |
Use the addition property of equality to rewrite the equation as an equivalent equation with
terms containing the specified variable on one side and all other terms on the other side. |
| Step 5. |
Use the distributive property and the multiplication property of equality to isolate the
specified variable. |
Now let's see how to apply these rules.
 |
Watch this animation explaining . |
Example 6: Solve A = (B + b)h for b.
Next, we will solve problems that can be modeled by known formulas. We use the same
problem-solving steps that were given in the previous section.
Now let's see how to apply these steps.
 |
Watch this animation explaining . |
| Example 7: |
Karen just received an inheritance of $10,000 and plans to place all the money
in a savings account that pays 5% interest compounded quarterly to help her son go
to college in 3 years. How much money will be in the account in 3 years? |
| |
|
| Solution: |
1. UNDERSTAND. Read and reread the problem. The appropriate formula needed to solve
this problem is the compound interest formula:
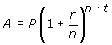
Be sure you understand the meaning of each of the variables in this formula:
A = amount in the account after t years
P = principal (or starting amount) invested
t = time in years
r = annual rate of interest (expressed as a decimal)
n = number of times compounded per year
2. TRANSLATE. Use the compound interest formula and let:
P = $10,000
r = 5% = 0.05
t = 3 years
n = 4
(n = 4 because the account is compounded quarterly, or 4 times per year.)
3. SOLVE the equation.
4. INTERPRET the results. Here, we check our work and state the solution.
Check your work: Repeat your calculations to make sure that no error was
made. Notice that $11,607.55 is a reasonable amount to have in an account after 3 years.
State the solution: In 3 years, the account will contain $11,607.55.
|
After completing this section, you should be able to:
- use interval notation
- solve linear inequalities using the addition property of inequality
- solve linear inequalities using the multiplication property of inequality
- solve problems that can be modeled by linear inequalities
A. Linear Inequalities in One Variable
A linear inequality is similar to an equation except that the equality symbol
is replaced with an inequality symbol, such as <, >, ≤, or ≥.
Linear Inequality in One Variable
A linear inequality in one variable is an inequality that can be written in
the form:
ax + b < c
where a, b, and c are real numbers and a ≠ 0.
This definition also holds for the inequality symbols >, ≤, and ≥.
A solution of an inequality is a value of the variable that makes the
inequality a true statement. The solution set of an inequality is the set
of all solutions.
For example, the solution set of the inequality:
x > 2
contains all numbers greater than 2, and can be written in set notation as:
{x | x > 2}
In these modules, we will use interval notation to write the
solution set. With this notation, the graph of:
{x | x > 2}
looks like:

and can be represented in interval notation as (2, ∞). Notice that the interval does
not include the number 2. The graph of:
{x | x ≥ 2}
looks like:
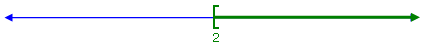
and can be represented in interval notation as [2, ∞).
The following table shows three equivalent ways to describe an interval: in set notation,
as a graph, and in interval notation.
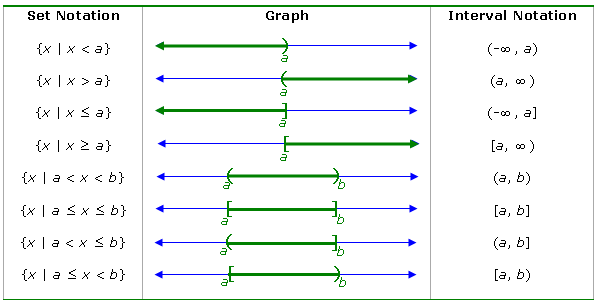
B. Addition Property of Inequalities
To solve a linear inequality, we use a process similar to the one used to solve a linear
equation. We use properties of inequalities to write successive equivalent inequalities until
the variable is isolated.
Addition Property of Inequality
Let a, b, and c represent real numbers.
If a < b, then a + c < b + c,
and a – c
< b – c.
This definition also holds for the inequality symbols ≤, >, and ≥.
In other words, the same number may be added or subtracted from both sides of an inequality
without changing the solution to the inequality.
Example 1: |
Solve 3x + 4 ≥ 2x – 6. Graph the solution
set. |
| |
|
| Solution: |
| 3x + 4 |
≥ |
2x – 6 |
Original problem. |
| 3x + 4 –2x |
≥ |
2x – 6 – 2x |
Subtracted 2x from both
sides. |
| x + 4 |
≥ |
–6 |
Combined like terms. |
| x + 4 – 4 |
≥ |
–6 –4 |
Subtracted 4 from both sides. |
| x |
≥ |
–10 |
Simplified. |
The solution set is {x | x ≥ –10}, which in interval notation is:
[–10, ∞)
The graph of the solution set is:
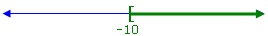
|
C. Multiplication Property of Inequality
To understand the multiplication property of inequality, let's start with the
true statement:
–3 < 7
and multiply both sides by a positive number.
–3 < 7
–3(2) <
7(2) Multiplied by 2.
–6 < 14 True.
The statement remains true when we multiply by 2. Next, let's multiply both sides of –3
< 7 by a negative number.
–3 < 7
–3(–2) < 7(–2) Multiplied by
–2.
6 < –14 False.
The statement is now false. However, if the direction of the
inequality symbol is reversed, the statement will be true.
6 > –14 True.
These examples lead to the multiplication property of inequality.
Multiplication Property of Inequality
If a, b, and c are real numbers,
and c is positive, then
a < b, and ac < bc
are equivalent inequalities.
If a, b, and c are real numbers, and c is
negative, then
a < b, and ac > bc
are equivalent inequalities.
This definition also holds for the inequality symbols ≤, >, and ≥.
In other words, when we multiply both sides of an inequality by the same
positive real number, the result is an equivalent inequality. When we multiply
both sides of an inequality by the same negative real number, however, we must
reverse the sign of the inequality symbol.
D. Solving a Linear Inequality in One Variable
To solve linear inequalities in general, follow the steps below.
Solving a Linear Inequality in One Variable
| Step 1. |
Clear the inequality of fractions by multiplying each side of the inequality by the
least common denominator. |
| Step 2. |
Use the distributive property to remove grouping symbols such as
parentheses. |
| Step 3. |
Combine like terms on each side of the inequality. |
| Step 4. |
Use the addition property of inequality to rewrite the inequality as an equivalent
inequality with variable terms on one side and numbers on the other side. |
| Step 5. |
Use the multiplication property of inequality to isolate the variable. |
Example 3: Solve –(x – 3) + 2 ≤ 3(2x – 5) +
x
| Solution: |
| –(x – 3) + 2 |
≤ |
3(2x – 5) + x |
Original equation. |
| –x + 3 + 2 |
≤ |
6x – 15 + x |
Applied the distributive property. |
| 5 –x |
≤ |
7x – 15 |
Combined like terms. |
| 5 – x + x |
≤ |
7x + x – 15 |
Added x to both sides. |
| 5 |
≤ |
8x – 15 |
Combined like terms. |
| 5 + 15 |
≤ |
8x – 15 + 15 |
Added 15 to both sides. |
| 20 |
≤ |
8x |
Combined like terms. |
 |
≤ |
 |
Divided both sides
by 8. |
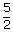 |
≤ |
x or
x ≥ 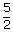 |
Simplified. |
Helpful Hint
Don't forget that 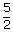 ≤ x is
the same as x ≥ ≤ x is
the same as x ≥ 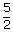 . .
The solution set written in interval notation is
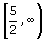 . Its graph is: . Its graph is:
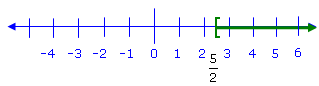
|
We conclude this section by looking at application problems that can be represented by an
inequality rather than an equation. We look for words such as "at least," "at most,"
"between," "no more than," and "no less than." In solving applications involving linear
inequalities, we use the same procedure we used when we solved applications involving linear
equations.
Example 4: |
Calculating Income with Commission |
| |
|
| |
A salesperson earns $600 per month plus a commission of 20% of his total sales. Find the
minimum amount of sales needed to receive a total income of at least $1,500 per month. |
| |
|
| Solution: |
1. UNDERSTAND. Read and reread the problem. Let x = amount of
sales.
2. TRANSLATE. As stated in the beginning of this example, we want the income greater than or
equal to $1,500. To write an inequality, notice that the sales income consists of $600 plus a
commission (20% of sales).
|
 |
| |
| |
3. SOLVE the inequality for x.
| |
| 600 + 0.20x |
≥ |
1,500 |
|
| 600 + 0.20x – 600 |
≥ |
1,500 – 600 |
Subtracted 600 from both sides. |
| 0.20 |
≥ |
900 |
Simplified. |
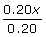 |
≥ |
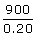 |
Divided both
sides by 0.20. |
| x |
≥ |
4,500 |
Simplified. |
4. INTERPRET. Here, we check our work and
state the solution.
Check your work: The income for sales of $4,500 is:
600 + 0.20(4,500), or $1,500
Therefore, if sales are greater than or equal to $4,500, then the income is greater than or
equal to $1,500.
State the solution: The minimum amount of sales needed for the salesperson
to earn at least $1,500 per month is $4,500 per month.
|
Now that we've solved simple linear inequalities (linear inequalities with one inequality
symbol in the expression), we are now ready to discuss compound linear inequalities.
After completing this section, you should be able to:
- find the intersection of two sets
- find the union of two sets
- solve the compound inequalities containing and
- solve compound inequalities containing or
A. Intersection of Two Sets
Intersection of Two Sets
The intersection of two sets, A and B, is the set of all elements common
to both sets.
A intersect B is denoted by:
A ∩ B
Example 1: |
Find A ∩ B if:
A = {x | x is an even number greater than 0 and less than
10}
B = {3, 4, 5, 6}
|
| |
|
| Solution: |
Let's list the elements in set A.
A = {2, 4, 6, 8}
The numbers 4 and 6 are in both sets A and B. Therefore, the
intersection is {4, 6}.
|
B. Union of Two Sets
Union of Two Sets
The union of two sets, A and B, is the set of all elements that belong to
either of the sets. A union B is denoted by:
A ∪ B
Example 2: |
Find A ∪ B if:
A = {x | x is an even number greater than 0 and less
than 10}
B = {3, 4, 5, 6} |
| |
|
Solution: |
As we saw in Example 1, A = {2, 4, 6, 8}. The numbers that are in
at least one of the sets A and B are {2, 3, 4, 5, 6, 8}. This
set is the union of A and B. |
To see animations illustrating these operations, click on the buttons below the picture
of sets A and B. The results of the operations are shaded in blue.
Figure 4.1
Intersection and Union
C. Solving Compound Inequalities
Two inequalities joined by the words and or or are called compound
inequalities.
For example:
| x – 7 < 2 and 2x + 1 < 9 |
is a compound inequality joined by the word and |
| 5x – 3 ≤ 10 or x + 1 ≥ 5 |
is a compound inequality joined by the word or |
The solution set of a compound inequality formed by the word and is
the intersection of the solutions sets of the two inequalities.
A value is a solution of the compound inequality if it is a solution of both
inequalities.
For example, the solution set of the compound inequality x ≤ 5 and
x ≥ 3 contains all values of x that make the inequality x ≤ 5
and the inequality x ≥ 3 true statements.
The graphs below illustrate the solution sets of each inequality, as well as the solution
set of the compound inequality.
| Set Notation |
Graph |
Interval Notation |
| {x | x ≤ 5} |
 |
(–∞, 5] |
| {x | x ≥ 3} |
 |
[3, ∞) |
| {x | 3 ≤ x ≤ 5} |
 |
[3, 5] |
We can write the solution set of the compound inequality in interval notation as [3, 5].
Example 3: |
Solve x – 7 < 2 and 2x + 1 < 9
|
| |
|
Solution: |
First we solve each inequality separately.
x - 7 < 2 and 2x
+ 1 < 9
x < 9
and 2x < 8
x < 9
and x < 4
Now we can graph the two intervals on two number lines and find their intersection. Their
intersection is shown on the third number line below:
|
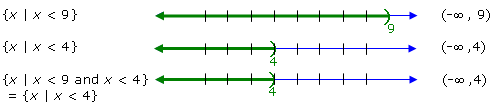
We can also write a compound inequality joined by the word and in compact form,
such as:
2 < 4 –x < 7
To solve this compound inequality, we isolate x in the "middle part." Because a
compound inequality is really two inequalities in one statement, we must perform the same
operations on all three parts of the inequality.
Example 4: |
Solve 2 < 4 – x < 7. |
| |
|
| Solution: |
To get x alone, we first subtract 4 from all three parts.

This is equivalent to –3 < x < 2.
The solution set in interval notation is (–3, 2), and its graph is shown below:

|
In some cases, the intersection of the solution sets may be empty, and the compound
inequality will have no solution.
Example 5: |
Solve 2x ≥ 0 and 4x – 1 ≤ –9. |
| |
|
| Solution: |
First, we solve each inequality separately.
2x ≥ 0 and 4x – 1 ≤ –9
x ≥ 0 and
4x ≤ –8
x ≥ 0 and
x ≤ –2
|
| |
| |
Now we can graph the two intervals and find their intersection.
|
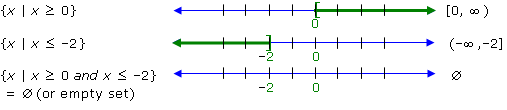
There is no number that is greater than or equal to 0 and
less than or equal to –2. Therefore, the solution set is ∅ (or
empty set).
The solution set of a compound inequality formed by the word or is the
union of the solution sets of the two inequalities. A value is a solution of
the compound inequality if it is a solution of either inequality.
For example, the solution set of the compound inequality x ≤ 1 or x ≥ 3
contains all numbers that make the inequality x ≤ 1 a true statement or the inequality
x ≥ 3 a true statement.
The graphs below illustrate the solution sets of each inequality as well as the solution set
of the compound inequality.
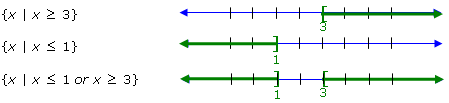
We can write the solution set of the compound inequality in interval notation as:
(–∞, 1] ∪ [3, ∞)
Example 6: Solve 5x – 3 ≤ 10 or x + 1 ≥ 5.
Solution: |
First, we solve each inequality separately.
5x – 3 ≤ 10 or x + 1 ≥ 5
5x ≤ 13 or x ≥ 4
x ≤ 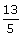 or
x ≥ 4 or
x ≥ 4
|
|
Now we can graph each interval and find their union. |
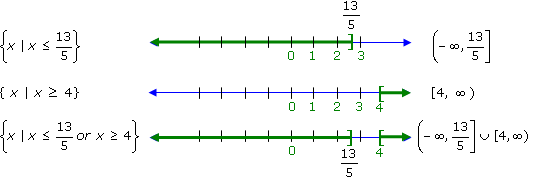
In some cases, the solution sets of each inequality overlap, and in such cases, the union
of the solution sets will be the set of all real numbers. In this particular example, there
is no overlap because there is no common portion of the intervals as you can see in the
graphs above.
After completing this section, you should be able to:
- solve absolute value equations
A. Solving Equations of the Form |x|= a
In module 1, we defined the absolute value of a number as its distance from 0 on a number
line. In this section, we concentrate on solving equations containing the absolute value of a
variable or variable expression. Examples of absolute value equations are:
- |x|= 3
- –5 = |2x + 7|
- |x – 5|= |3x + 1|
For the absolute value equation |x|= 3, the solution set contains all numbers whose
distance from 0 is 3 units. Two numbers are 3 units away from 0 on the number line: 3 and –3, as
shown below:
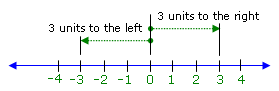
Thus, the solution set of the equation |x|= 3 is {3, –3}.
Solving Equations of the Form |x| = a
If a is a positive number, then |x| = a is equivalent to
x = a or x = –a.
Note that if a is a negative number, the equation has no solution because absolute
value is a distance from 0, and it is not possible to have a negative distance. Also
note that x can be a single variable or a variable expression.
| |
|
Example 1: |
Solve |5w + 3|= 7 |
| | |
Solution: |
In this example, the expression inside the absolute value bars is:
5w + 3
If we think of the expression 5w + 3 as x in the absolute-value
property, we see that |x|= 7 is equivalent to:
x = 7
or x = –7
Then we substitute 5w + 3 for x, and we have:
5w + 3 = 7 or
5w + 3 = –7
Now we solve these two equations for w.
5w + 3 = 7 or
5w + 3 = –7
5w = 4
or 5w = –10
w = 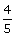 or
w = –2 or
w = –2
|
| |
|
|
Check: To check, first substitute –2 for w and then substitute
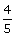 for w in the original equation, |5w + 3|= 7.
for w in the original equation, |5w + 3|= 7.
Let w = –2:
Let w = 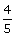
|5(–2) + 3| = –7 |5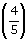 + 3| = 7 + 3| = 7
|–10 + 3| = 7 |4 + 3| = 7
|–7| = 7 |7| = 7
7 = 7 True. 7 = 7 True.
Both solutions lead to true statements. Therefore, the solutions are –2 and 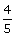 and
the solution set is
and
the solution set is 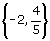 . .
|
The next example illustrates a special case for absolute value equations: the absolute
value, when isolated, is equal to a negative number.
| Example 2: |
Solve 2|x| + 25 = 23. |
| |
| Solution: |
First isolate the absolute value.
| 2|x| + 25 |
= |
23 |
Original equation. |
| 2|x| |
= |
–2 |
Subtracted 25 from both sides. |
| |x| |
= |
–1 |
Divided both sides by 2. |
|
| |
The absolute value of a number is never negative, so this equation has no solution. The
solution set is { } or ∅.
|
B. Solving Equations of the Form |x|= |y|
Two absolute value expressions are equal if the expressions inside the absolute value bars
are equal to each other or are opposites of each other.
| Example 3: |
Solve |3x + 2|= |5x – 8|. |
| |
| Solution: |
This equation is true if the expressions inside the absolute value bars are equal to each
other or are opposites of each other.
Solve each equation:
| 3x + 2 = |
5x –8 |
or |
3x + 2 = |
–(5x – 8) |
| –2x + 2 = |
–8 |
or |
3x + 2 = |
–5x + 8 |
| –2x = |
–10 |
or |
8x + 2 = |
8 |
| x = |
5 |
or |
8x = |
6 |
| x = |
5 |
or |
x = |
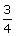 |
|
| |
The solutions are 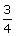 and 5. We can check our answers by substituting 5 for x and
then and 5. We can check our answers by substituting 5 for x and
then 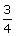 for x in the original equation: for x in the original equation:
|3x + 2|= |5x – 8|
We will leave checking these solutions for you to do.
|
Note: If we had solved only for the expressions inside the absolute value bars being equal
to each other, we would have omitted the second solution to the equation, namely, the solution
that results from setting the left side equal to the opposite of the right side. It is
important to remember when solving absolute value expressions that you must solve two
equations.
After completing this section, you should be able to do the following:
- solve absolute value equations of the form |x| < a
- solve absolute value equations of the form |x| > a
A. Solving Absolute Value Inequalities of the Form |x| < a
The solution set of an absolute value inequality such as |x| < 2 contains all
numbers whose distance from 0 is less than 2 units, as shown below.
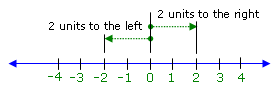
We graph this solution set by indicating rounded parentheses at the endpoints (because
the endpoints are not included) and drawing a line to represent the space between the
endpoints.
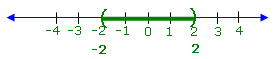
The solution set is:
{x | –2 < x < 2}
or, in interval notation:
(–2, 2)
Below, we give the rule for solving absolute value inequalities of the form |x|
< a.
Solving Absolute Value Inequalities of the Form
|x| < a
If a is a positive number, then |x| < a is equivalent to
–a < x < a.
Note that if a is a negative number, the inequality has no solution. Also note
that x can be a single variable or a variable expression.
Now let's see how to apply this rule.
 |
Watch this animation explaining . |
B. Solving Absolute Value Inequalities of the Form
|x| > a
The solution set of an absolute value inequality such as |x| ≥ 3 contains all
numbers whose distance from 0 is 3 or more units. This distance can be in either
the positive or in the negative direction. The graph of the solution set
contains the number 3 and all points to the right of 3 on the number line, and
–3 and all points to the left of -3 on the number line, as shown below.
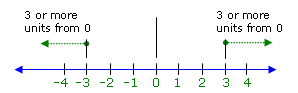
This graph represents the collection of points that begin 3 units from 0 (at
–3 and 3) and continue away from 0 (hence having a distance of 3 or more from 0
in both directions).
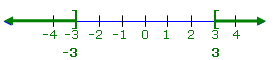
The solution set is:
{x | x ≤ –3 or x ≥ 3}
or, in interval notation:
(–∞, -3] ∪ [3, ∞)
Below, we give the rule for solving absolute value inequalities of the form |x|
> a.
Solving Absolute Value Inequalities of the form
|x| > a
If a is a positive number, then |x| > a is equivalent to x
< –a or x > a.
Note that if a is a negative number, the solution set is all real numbers. Also
note that x can be a single variable or a variable expression.
We have concluded our discussion of solving absolute value inequality expressions. Now try
the problems in the self-assessment section of this module to see how well you understand the
concepts that you've just covered. The self-assessment problems are not graded, but
are a useful tool to determine which concepts you've mastered and
which concepts you may wish to review before moving forward.
Return to top of page