Module 5: Polynomials

Topics

1. Exponents
2. Polynomials
3. Factoring Polynomials

I. Exponents

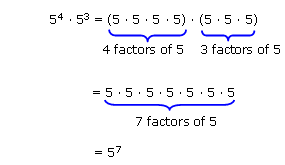
After completing this section, you should be able to do the following:

• use the product rule, quotient rule, and power rule of exponents
• use the power rules for products and quotients
• evaluate a number raised to the 0 power
• evaluate numbers raised to negative integer powers
• use the rules and definitions for exponents to simplify exponential expressions
• write numbers in scientific notation
• convert numbers from scientific notation to standard form
• perform operations with numbers written in scientific notation

Recall from module 1 that an exponent is a shorthand notation for repeated factors. For example:

2 · 2 · 2 · 2 · 2

can be written as 2⁵. The expression 2⁵ is called an exponential expression, where 2 is the base and 5 is the exponent. We can also use exponential notation with variables, as was shown in module 2. Thus, x · x · x · x · x can be written as x⁵.

Exponential expressions can be multiplied, divided, or raised to a power. We will now discuss the rules for these operations.

A. Product Rule for Exponents

Let's look at the two examples below to see if we can discover a rule for multiplication of factors with exponents.

Example 1:

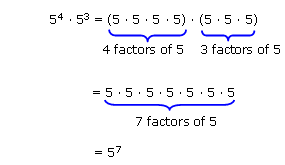
Example 2:

x² · x³ = (x · x) · (x · x · x)

            = x · x · x · x · x

            = x⁵

In both cases, notice that the result is exactly the same if the exponents are added, which suggests the following rule.

Now let's look at one more example.

Example 3:    Use the product rule to simplify (7y⁴)(–3y²).

Solution:      

B. Quotient Rule for Exponents

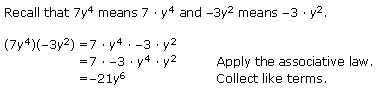
Another pattern for simplifying exponential expressions involves quotients. To simplify an expression such as , in which the numerator and denominator have a common base, we can apply the fundamental principle of fractions and divide the numerator and the denominator by the common base factors. Assume for this discussion that the denominators are not equal to 0.

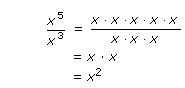
Notice that the result is exactly the same if we subtract the exponents of the common bases.

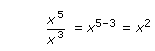
We can now state a rule for division with exponents.

Example 4:
Solution:	Begin by grouping common bases. Remember that there is an understood exponent of 1 when no exponent is written.

C. Power Rules for Exponents

Exponential expressions can themselves be raised to powers. Let's see how to simplify an expression like (x²)³.

By definition:

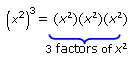
which can be simplified by the product rule of exponents:

(x²)³ = (x²)(x²)(x²) = x²⁺²⁺² = x⁶

Notice that the result is exactly the same if we multiply the exponents:

(x²)³ = x^2·3 = x⁶

The following property generalizes this result.

Watch this animation explaining how to use the power rule for exponents.

When the base of an exponential expression is a product or quotient, the definition of an exponent still applies. For example:

(xy)³ = (xy)(xy)(xy)
         = x · x · x · y · y · y
         = x³y³

Notice that we raise each factor within the parentheses to a power of 3, which leads to the following rule.

Let's see what happens when we raise a quotient to a power. For example:

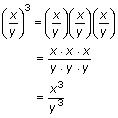
Notice here that we raised both the numerator and denominator to a power of 3. In general, we have the following rule.

All three power rules can be combined to simplify exponential expressions.

Example 5:
Solution:

D. Zero Exponent

Let's now give meaning to an exponential expression that has a zero exponent, such as x. To do so, we will simplify in two ways and compare the results.

From these results, we conclude that x = 1, as long as x itself is not 0. In general, any base raised to the 0 power is equal to 1, as long as the base does not have a value of 0.

E. Negative Exponents

So far, we have only looked at exponents that are positive integers or 0. In this section, we give meaning to expressions with negative exponents, such as x^–3.

Suppose that we wished to simplify the expression. Using the quotient rule for exponents, we subtract exponents:

We can also use the definition of an exponent to simplify .

If the quotient rule is to hold true for negative exponents, we conclude that x^–3 must equal . The general rule is stated below.

Watch this animation explaining how to evaluate numbers raised to negative integer powers.

Example 7:	Write each expression using only positive exponents.
a.	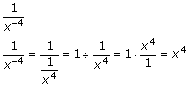Notice that the effect of a negative exponent is to take the reciprocal of the exponential expression and change the sign of the exponent. Another way to look at this is to recognize that the negative exponent causes the exponential expression to change its position from denominator to numerator (and vice versa), and then change the sign of its exponent.
b.
c.
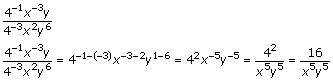d.

F. Scientific Notation

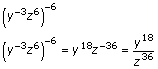Both very large and very small numbers frequently occur in many fields of science. For example, the distance between the sun and the planet Pluto is approximately 5,906,000,000 kilometers, and the mass of a proton is approximately 0.00000000000000000000000165 grams. It can be tedious to write these numbers using decimal notation, so scientific notation is used as shorthand for expressing very large and very small numbers.

First, let's look at the form for scientific notation.

Now let's look at the steps involved in writing a number in scientific notation.

Example 8: Write each number in scientific notation.

a.     367,000,000

Step 1.  Move the decimal point until the number is between 1 and 10.

Step 2.  The decimal point is moved 8 places, and the original number is
            greater than 10, so the count is positive 8.

Step 3.  367,000,000 = 3.67 × 10⁸.

b.     0.00000000239

Step 1.  Move the decimal point until the number is between 1 and 10.

Step 2.  The decimal point is moved 9 places, and the original number
             is less than 1, so the count is negative 9.

Step 3.  0.00000000239 = 2.39 × 10^–9.

A number written in scientific notation can be rewritten in standard form by moving the decimal point the same number of places as the exponent of 10. For example, to write 2.95 × 10³ in standard form, recall that 10³ = 1,000. Thus,

2.95 × 10³ = 2.95 × 1,000 = 2,950

Similarly, if the exponent is negative, we make use of the definition of a negative exponent.

Notice that we move the decimal point to the right when the exponent of 10 is +3, and we move the decimal point to the left when the exponent of 10 is –3. We generalize this rule as follows:

Performing operations on numbers written in scientific notation makes use of the rules and definitions for exponents that we discussed earlier.

Example 10:	Perform each indicated operation. Write each result in standard form, without exponents.
a.
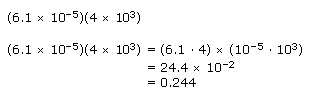b.

II. Polynomials

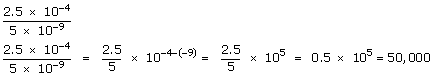After completing this section, you should be able to do the following:

• define monomial, binomial, trinomial, polynomial, and degree
• add and subtract polynomials
• multiply polynomials
• divide polynomials

A. Introduction to Polynomials

In module 2, we discussed algebraic expressions, and learned how to add, subtract, and multiply these expressions. In this section, we continue the discussion with a special algebraic expression called a polynomial. First, let's review some definitions presented in module 2.

Recall that a term is a number, or the product of a number and variables raised to powers. For example, the terms of the expression 4x² + 3x – 5 are 4x², 3x, and –5.

The coefficient of a term is the numerical factor. In the example above, the coefficient of the first term is 4, the coefficient of the second term is 3, and the coefficient of the third term is –5. Below, we use our understanding of terms to help define a polynomial.

For example, 2x² + 9 is a polynomial, but 5x^–2 – 5y is not. Why not?

Some polynomials are given special names depending on the number of terms.

• A monomial is a polynomial with exactly one term.
• A binomial is a polynomial with exactly two terms.
• A trinomial is a polynomial with exactly three terms.

Each term of a polynomial has a degree. The degree of a term is the sum of the exponents on the variables contained in the term. The degree of a constant is 0. The degree of a polynomial is the greatest degree of any term of the polynomial.

B. Adding and Subtracting Polynomials

In module 2, you learned how to simplify algebraic expressions by combining like terms. Because polynomials are special instances of algebraic expressions, the techniques you learned that apply to expressions also apply to polynomials. To add or subtract polynomials, you will simply combine like terms.

C. Multiplying Polynomials

In module 2, you learned how to multiply algebraic expressions by using the associative and distributive properties. We will extend these techniques in this section to learn how to multiply any two polynomials together.

To multiply two monomials such as (–5x³) and (–2x⁴), recall that you use the associative and commutative properties of multiplication to regroup the factors. Use the product rule of exponents to multiply the variable factors.

(–5x³)(–2x⁴) = (–5)(–2)(x³)(x⁴) = 10x⁷

To multiply a monomial by a polynomial, recall that you use the distributive property:

a(b + c) = ab + ac

We also use the distributive property to multiply two binomials. For example, to multiply (x + 3) by (x + 1), distribute the factor (x + 3) first.

(x + 3)(x + 1) = x(x + 1) + 3(x + 1)              Distribute (x + 3).        
                      = x(x) + x(1) + 3(x) + 3(1)     Distribute again.
                      = x² + x + 3x + 3                   Multiply.
                      = x² + 4x + 3                         Combine like terms.

Notice that in the second step, each term in the first binomial is multiplied by each term in the second binomial. This technique can be expanded and applied to the multiplication of any two polynomials.

D. Dividing Polynomials

Now that we know how to add, subtract, and multiply polynomials, we will learn how to divide polynomials. To divide a polynomial by a monomial, recall from module 1 the process for adding fractions. We add fractions that have a common denominator by adding the numerators and putting the sum over the common denominator:

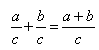
If we read this statement from right to left, and let a, b, and c be monomials, with c not equal to zero, we have the following method for dividing a polynomial by a monomial.

Example 6:	Divide:
Solution:

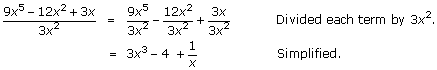To divide a polynomial by a polynomial with more terms than a monomial, we use a process called long division. Doing long division with polynomials is similar to doing long division with numbers. The long-division algorithm has four steps, which are repeated until the problem is finished.

Let's review the steps in arithmetic long division.

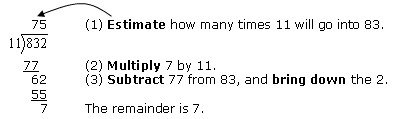
The following steps can help you remember the division algorithm and apply it to polynomial long division:

Step 1.  Estimate.
Step 2.  Multiply.
Step 3.  Subtract.
Step 4.  Bring down.

Example 7:	Divide: using long division.
Solution:	The quotient is x + 4.

Example 8:	Divide: using long division.
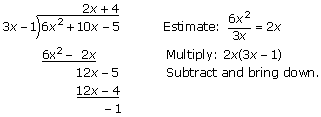
Solution:	The quotient is 2x + 4 with a remainder of –1. This can be written as:

III. Factoring Polynomials

After completing this section, you should be able to do the following:

• factor out the greatest common factor (GCF) from a polynomial
• factor a polynomial by grouping

A. Factoring out the GCF from a Polynomial

In module 1, we introduced to the concept of factoring, and in module 2, we extended this concept to factoring out the greatest common factor from an algebraic expression. As we have seen in the previous section, many of the expressions that we deal with are actually polynomials. Therefore, to factor out the greatest common factor from a polynomial, we apply the techniques presented in module 2.

Let's review with an example from module 2:

B. Factoring a Polynomial by Grouping

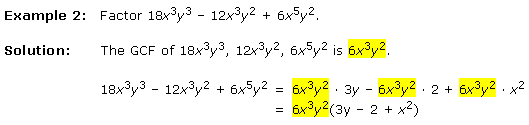
Once the GCF is factored out, we can often continue to factor the polynomial using a technique called grouping.

We can summarize the steps in factoring by grouping as follows.

Let's look at one more example.

Return to top of page