Module 8: Rational Exponents and Rational Expressions

Topics

1. Radicals and Radical Functions
2. Rational Exponents
3. Simplifying Radical Expressions
4. Arithmetic Operations with Radical Expressions
5. Rationalizing Denominators and Numerators of Radical Expressions
6. Radical Equations and Problem Solving
7. Complex Numbers

I. Radicals and Radical Functions

After completing this section, you should be able to:

• find square roots of perfect squares
• approximate square roots of non-perfect squares
• find cube roots
• find nth roots
• use absolute value to find the even roots of real numbers
• graph the square-root and cube-root functions

A. Finding Square Roots

To find the square root of a number a, think of a number that when multiplied by itself will equal a. In other words, the square root of a is one of two equal factors of a. For example, one square root of 25 is 5 because:

5 · 5 = 5² = 25

Another square root of 25 is –5 because:

(–5) (–5) = (–5)² = 25

We denote the nonnegative, or principal, square root with the radical sign:

We denote the negative square root with a negative radical sign:

An expression containing a radical is called a radical expression. The expression under the radical sign is called a radicand.

Let's summarize these concepts.

We have already seen that to find the square root of a number a, we think of a number that when multiplied by itself will equal a. But how do we find the square root of a variable raised to an exponent? It's easy if we remember that when we multiply, we add exponents. So to find the exponent of the square root, we only have to divide the variable's exponent in half.

Study the examples below (for simplicity, we assume all variables represent positive numbers):

= x10/2 = x5	Remember that x5 · x5 = x10.
= x8/2 = x4	Remember that x4 · x4 = x8.
= x22/2 = x11	Remember that x11 · x11 = x22.

Now try some examples yourself to become familiar with these ideas.

Example 1:	Find the square roots. (Assume all variables represent positive numbers.)
	a.	Solution
	b.	Solution
	c.	Solution
	d.	Solution
	e.	Solution
	f.	Solution
	g.	Solution
	h.	Solution

B. Approximating Square Roots Using a Calculator

Numbers such as 1, 4, 9, 16, and 25 are called perfect squares because each is the square of a rational number. Therefore, square roots of perfect squares are equal to rational numbers.

The square root of a number that is not a perfect square, such as , is not a rational number. It is an irrational number, and we can find its decimal approximation using a calculator. For example, is approximately equal to 1.732, as written below.

Example 2:	Use a calculator to approximate . Round your answer to three decimal places. You can find an approximation for any square root by keying the number into the calculator and pushing the square-root button.
Solution:	Using a calculator,

C. Finding Cube Roots

The method we use to find square roots can be extended to find higher-order roots, such as cube roots. The cube root of a number is one of the three equal factors of the number. For example, the cube root of 8 is 2 because:

2 · 2 · 2 = 2³ = 8

We indicate the cube root as follows:

= 2

Remember that when we found the square root of a variable raised to an exponent, we divided the exponent by 2. Now, to find the cube root of a variable raised to an exponent, we divide the exponent by 3. The examples below will help you understand this concept.

= x3/3 = x	Remember that x1 · x1 · x1 = x3.
= x30/3 = x10	Remember that x10 · x10 · x10 = x30.
= 10x12/3 = 10x4	Remember that 10x4 · 10x4 · 10x4 = 1,000x12.

Now practice finding cube roots to ensure you understand this concept.

Example 3:	Find the cube roots.
	a.	Solution
	b.	Solution
	c.	Solution
	d.	Solution
	e.	Solution

D. Finding nth Roots

We can extend our discussion of square roots and cube roots to include roots other than these two. The nth root of a number a, where n is a natural number greater than 1, is written:

The number n is called the index, and is usually not shown when we indicate square roots, where n = 2.

We find the nth root of a number or a variable raised to an exponent in the same way we find square and cube roots. To find the nth root of a number, we find a number that when raised to the nth power, gives the original number. In other words, the nth root of a number is one of n equal factors of the number. In the case of a variable raised to an exponent, we divide the exponent by n.

For example (for simplicity, we assume all variables are positive):

= x25/5 = x5	because  x5 · x5 · x5 · x5 · x5 = (x5)5 = x25
	because  2 · 2 · 2 · 2 · 2 = (2)5 = 32
	because  (–2x2)(–2x2)(–2x2) = (–2x2)3 = –8x6

Now try some examples yourself.

Example 4:	Find the indicated roots.
	a.	Solution
	b.	Solution
	c.	Solution
	d.	Solution

E. Find , Where x is a Real Number

We will now look at the cases when the index of the radical is even, and there are variables in the radicand. If we restrict the variables to positive numbers, then the resulting root will be positive.

If the variables are negative numbers, however, we must use absolute-value bars to ensure that the result is a positive number. For example, we write:

to ensure that the result is positive. The same situation occurs when the index is any even number. Note that when the index is an odd number, absolute-value bars are not necessary. Why?

Try to work out the solutions to the examples below, then look at how we found the answers.

Example 5:	Find the roots. Variables may represent any real number.
	a.
	b.
	c.
	d.
Solution:	a.
	b.
	c.
	d.  (Note that absolute-value bars are not needed in part d because the index is odd.)

F. Graphing Square- and Cube-Root Functions

The square-root and cube-root operations can be represented by the functions:

f(x) = and g(x) =

We know that the square root of a negative number is not a real number. Therefore, the domain of the square-root function is the set of all nonnegative real numbers. The domain of the cube-root function, however, is the set of all real numbers because the index is odd.

Now look at the graphs of the two functions and .

Example 6:	Graph the square root function f(x) = .
Solution:	We know that the domain is the set of all nonnegative real numbers. Therefore, we evaluate the function for several values of +x, plot the resulting points, and connect the points with a smooth curve. Figure 8.1 Graph of f(x) =

Example 7:	Graph the function f(x) =
Solution:	The domain of this function is the set of all real numbers. As before, we will evaluate the function for several values of x, both positive and negative. Then we plot the points and connect them with a smooth curve. Where needed, we will use a calculator to approximate values. Figure 8.2 Graph of f(x) =

II. Rational Exponents

After completing this section, you should be able to:

• define a^1/n, a^m/n, and a^–m/n
• simplify expressions with rational exponents
• use rational exponents to simplify radical expressions

A. Definition of a^1/n

In this section, we will study expressions that have non-integer exponents, such as 3^1/2 or x^2/3. We will define these expressions so that all the existing rules for exponents will also apply when the exponents are rational numbers.

Let's begin by looking at 5^1/3. Let:

x = 5^1/3

Then, by cubing both sides of this equation, we obtain:

x³ = (5^1/3)³
x³ = 5

From this equation, we can deduce that x is the number whose cube is 5, or:

x =

This equation leads us to conclude that 5^1/3 = .

We can use this definition to solve the problems below.

B. Definition of a^m/n

Next, we will expand the discussion of rational exponents to include exponents such as . As before, we define the meaning of these exponents so that the rules for exponents still hold true.

Now look at the exponential expression 8^2/3 in two different ways.

Based on the above, we can see that it does not matter whether you:

1. raise the base to a power first and then take the nth root

   or

2. take the nth root first and then raise the base to a power

Now let's apply this definition to the problems below. Try to work out the solutions yourself, then look at our answers.

C. Definition of a^–m/n

Finally, we will discuss the case when the rational exponent is negative.

Study the examples below to see how we use this definition.

Example 3:	Write each expression with a positive exponent and simplify.
	16–3/4 –27–2/3
Solution:

D. Simplifying Expressions with Rational Exponents

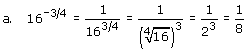
The rules for exponents that were developed in module 6 also apply when the exponents are rational numbers. Thus, we can use these rules when simplifying expressions that contain rational exponents. For the remainder of this module, we will assume that variables represent positive real numbers, so that we do not need to use absolute-value bars when simplifying even roots.

For your convenience, we summarize the exponent rules below.

• a^m · aⁿ = a^m+n
• a^m/aⁿ = a^m–n
• (x^m)ⁿ = x^mn
• (xy)^m = x^my^m
• (x/y)^m = x^m/y^m

We can apply these rules to examples using rational exponents. Try these examples yourself, and then look at our solutions below. Write the answers with all positive exponents.

E. Using Rational Exponents to Simplify Radical Expressions

Some radical expressions are easier to simplify if we first change them to rational exponents. Then, use the properties of exponents to simplify the exponents, and finally, change the expression back to radical notation.

Let's see how to do this by simplifying .

	Original expression.
(x4)1/8 = x4/8	Changed to an exponential expression.
x1/2	Simplified the exponent by reducing the fraction.
	Changed back to radical notation.

Now try some of these examples yourself before looking at our solutions.

III. Simplifying Radical Expressions

After completing this section, you should be able to:

• use the product rule for radicals
• use the quotient rule for radicals
• simplify radical expressions

Because radicals can be written as exponential expressions with rational exponents, it follows that the rules for exponents also apply to radicals. In particular, we will look at the product rule and quotient rule.

A. Using the Product Rule for Radicals

To verify that the product rule for radicals is valid, study the following:

These two examples show that , which leads to the following rule.

Now try to apply this rule.

Example 1:	Multiply.
	a.          Solution b.          Solution
The next example is a little more complicated, so we have worked out the solution for you.
	c.

B. Using the Quotient Rule for Radicals

We will verify that the quotient rule for radicals is similar to the quotient rule for exponents. Study the two examples below.

These examples show that:

We can express these findings as the rule below.

Now try to apply this rule.

Example 2:	Use the quotient rule to simplify.
	a.  Solution b.    Solution
The next example is a little more complicated, so we will work out the solution for you.
	c.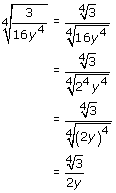

C. Simplifying Radicals

We can use both the product and quotient rules to simplify a radical.

Study the following examples.

Now try some examples yourself.

Example 3:	Simplify.
	a. Solution b. Solution

Notice that in each case, we simplified the radical so that there are no perfect nth powers in the radicand. For example, if we are simplifying a square root, we make sure that the radicand does not contain any perfect squares. In general, we say that a radicand of the form is simplified when the radicand a contains no factors that are perfect nth powers (other than 1 or –1).

Study the examples below to be sure you understand this process.

Example 4:	Use the quotient rule to simplify.
	a.

IV. Arithmetic Operations with Radical Expressions

After completing this section, you should be able to:

• add, subtract, and multiply radical expressions

A. Adding or Subtracting Radical Expressions

Previously, we learned that we can add or subtract like terms by using the distributive property. Similarly, we can use the distributive property to add or subtract like radicals. We begin by defining like radicals as radicals with the same index and the same radicand. Let's look at the following examples to discover the rule for adding and subtracting like radicals.

From these examples, it can be seen that adding or subtracting like radicals is simply a matter of adding or subtracting the coefficients of the like radicals.

Try to do these examples yourself, then look at our solutions.

Example 1:	Simplify. Assume that variables represent positive real numbers.
Solution:	a.  Problem.     Factored under the radical so that one of the factors is a perfect cube.     Wrote perfect cubes in exponential form.     Simplified by taking perfect cubes out from under the radical.     Multiplied 2 times 5.     Combined like terms.     b.

B. Multiplying Radical Expressions

To multiply radical expressions, we can use many of the same properties that were used to multiply polynomial expressions. For example, we can use the distributive property in the problem below.

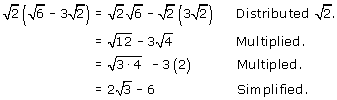
We can also use the formula for the square of a binomial or the FOIL method to multiply binomials that contain radicals. Study the examples below to be sure you understand this process.

Example 2:

Multiply. a.   Problem.                Applied FOIL method.                Multiplied.     b.   Problem.                 = Expanded form.                 = Multiplied binomials.                 = Multiplied.                 = Simplified.

V. Rationalizing Denominators and Numerators of Radical Expressions

After completing this section, you should be able to:

• rationalize denominators and numerators of radical expressions

A. Rationalizing Denominators that Have One Term

In this section, we look at division of radical expressions. When we divide radical expressions such as , we usually want to write the result either without a radical in the denominator or without a radical in the numerator. The process of writing this expression without a radical in the denominator is called rationalizing the denominator because the denominator in the expression will only contain rational expressions.

To rationalize the denominator of , we use the fundamental principle of fractions and multiply both the numerator and the denominator by.

Try the examples below yourself, then look at our solutions.

Example 1:	Rationalize the denominator of each expression.
	a.  b.  c.
Solution:	a.  b.  c.

B. Rationalizing Dominators that Have Two Terms

When the denominator of a radical expression contains two terms, we must use a different method to rationalize the denominator. Recall that if we multiply the sum and difference of two radicals, the result does not contain any radicals.

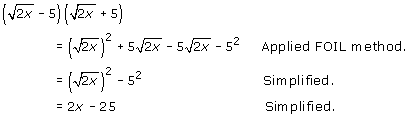
Note that in this example, there are no radical signs in the answer because the two middle terms added to zero, as they always do when the sum and difference of two identical terms are multiplied. This observation will be useful when rationalizing the denominators of radical expressions.

We call and conjugates of each other. The example below shows how we can use conjugates to rationalize the denominator.

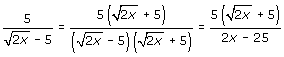
Now study the examples below to become familiar with this process.

Example 2:	Rationalize each denominator.

C. Rationalizing Numerators

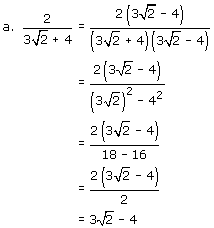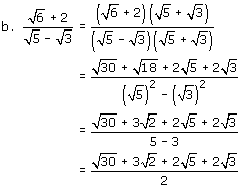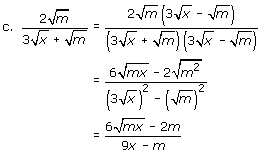We now look at the process of rationalizing the numerator. This process is similar to that of rationalizing the denominator.

VI. Radical Equations and Problem Solving

After completing this section, you should be able to:

• solve radical equations
• use the Pythagorean theorem to model problems

A. Solving Equations that Contain Radical Expressions

In this section, we look at methods for solving equations containing radical expressions. We will use the power rule to solve these equations.

Notice that this property states that the solutions of the new equation may not be solutions of the original equation. Therefore, each solution of the new equation must be checked to make sure it is also a solution of the original equation. If a proposed solution is not a solution of the original equation, it is called an extraneous solution.

Study the example below to see how to solve a radical equation.

Example 1:	Solve
Solution:	Use the power rule to square both sides of the equation. Check this solution in the original equation. Therefore, the solution set is {42}.

We summarize this process below.

Now let's apply this process to a more difficult problem.

Example 2:	Solve
Solution:	First, isolate the radical term by subtracting 5 from each side of the equation. Next, raise both sides to the third power to eliminate the radical. Now we must check the solution by substituting –9 for x in our original equation, which was .                 Original equation.                 Substituted –9 for x.                 Simplified under the radical sign. –2 + 5 = 3                 Took cube root of –8.    3 = 3   True.      Compared. The solution checks in the original equation, therefore, the solution set is {–9}.

Example 3:	Solve
Solution:	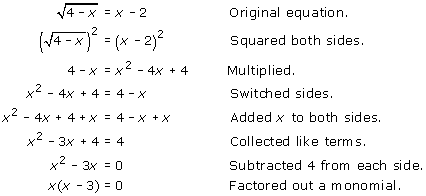x =    or   x – 3 = 0      Set each factor equal to 0.                       x = 3 There are two solutions to this equation, and we must check both. Check x = 0:     Check x = 3:     The solution 0 does not check, so 0 is an extraneous solution. Therefore, the solution set is {3}.

Example 4:	Solve
Solution:	First, isolate one radical. It is best to isolate the more complicated one. Next, square both sides and do the multiplication. Now, isolate the remaining radical by following the steps above.    Added –9 – 2x                    Collected like terms.               Switched sides.            36(2x) = 16    Squared both sides.                72x = 16    Multiplied 36(2x)                      Divided by 72. The proposed solution checks in the original equation, so the solution set is .

B. Using the Pythagorean Theorem to Model Problems

First, refresh your memory about the Pythagorean theorem.

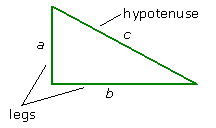
Now let's see how we use this theorem. First, we'll practice just using the theorem, then we'll apply it to a real-world problem.

VII. Complex Numbers

After completing this section, you should be able to:

• define imaginary and complex numbers
• add or subtract complex numbers
• multiply complex numbers
• divide complex numbers
• raise the complex number i to powers

A. Imaginary and Complex Numbers

Earlier in this module, we saw that the square root of a negative number is not a real number. For example, is not a real number because no real number exists whose square is –16.

In this section, we discuss a number system that includes roots of negative numbers. This number system is called the complex number system, and it includes the set of real numbers as a subset. The complex number system allows us to solve equations such as x² + 1 = 0 that have no real-number solutions. To begin our study of the complex number system, we define the imaginary unit i.

Using this definition, we can write the square root of a negative number in terms of i. For example,

Let's practice using the i notation.

Example 1:

Express in terms of i. Solution Solution Solution

Now that we have defined imaginary numbers, we can define complex numbers.

Notice that the set of real numbers is a subset of the complex numbers because any real number can be written in the form a + 0i—a complex number.

a + bi is a real number when b = 0. A complex number is called a pure imaginary number if a = 0.

The following diagram shows the relationship between complex numbers and their subsets.

Figure 8.5
Hierarchy of Numbers

Adding or Subtracting Complex Numbers

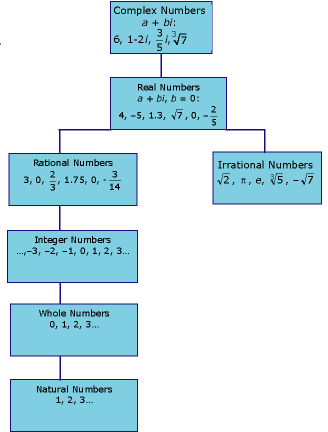
Complex numbers can be added or subtracted by adding or subtracting their real parts, and then adding or subtracting their imaginary parts.

Let's look at the rules for these operations.

Now apply these rules to the examples below, then look at our solutions.

C. Multiplying Complex Numbers

We can use the distributive property to multiply complex numbers in the same way we have used it previously. Also, we multiply two complex numbers the same way we multiply two binomials—by using the FOIL method or the rules for special products. Then, we use the relationship i² = –1 to complete the multiplication process.

Work out the examples below, then look at our solutions.

D. Dividing Complex Numbers

Notice that in the last example (part d of example 3), the result is a real number. The complex numbers 7 + 3i and 7 – 3i are complex conjugates of one another. When complex conjugates are multiplied, the result is always a real number. A general rule for complex conjugates is given below.

We will use complex conjugates to divide the complex numbers in the examples below. Study these examples to be sure you understand the process.

Example 4:	Divide. Write the result in the form a + bi.
	a.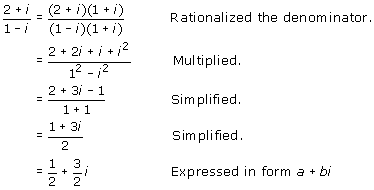
	b.

E. Raising i to Higher Powers

Finally, let's examine what happens when we raise the imaginary unit i to an exponent greater than 2. Observe the pattern below.

i² = –1
i³ = i² · i = (–1) · i = –i
i⁴ = i² · i² = (–1) · (–1) = 1
i⁵ = i⁴ · i = (1) · i = i
i⁶ = i⁴ · i² = (1) · (–1) = –1
i⁷ = i⁴ · i³ = (1) · –i = –i
i⁸ = i⁴ · i⁴ = (1) · (1) = 1
i⁹ = i⁴ · i⁴ · i = (1) · (1) · i = i

Notice that this pattern repeats every 4^th power. Thus, to find higher powers of i, we use the fact that i⁴ = 1, and rewrite the power of i in terms of i⁴.

Study the following example.

i²² = i²⁰ · i²
= i⁴· i⁴ · i⁴ · i⁴ · i⁴ · i²
= (i⁴)⁵ · i²
= (1) · (1) · (1) · (1) · (1) · (–1)
= –1

Now try two examples for yourself. Solving the problems below will help you become familiar with the concept of imaginary numbers.

Return to top of page