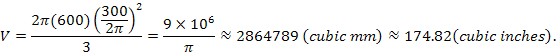Exercise 2 Solution

(You may want to maximize your window to see the solution more clearly.)

Let's first work the problem for a general ellipse  (see figure 2(b)).

Figure 2(b)

Revolving this ellipse about the x‑axis will result in a circular cross section for the disk method, giving a volume of:

Here, the symmetry was used to split the interval of integration. Integrating gives,

(Compare this solution with the standard volume formula of an ellipsoid.)

To determine our volume, we need the values of a and b for a standard rugby football. Note that the length of the ball is 2a, and the radius in the middle cross section is b (see figure 2(b), above).

Checking reference sources (for example, the Internet), we determine these values to be approximately a = 600 mm and  (Note: Official rugby rules allow for variation in these dimensions.) Thus the volume is (approximately),