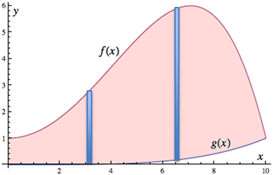
Any vertical rectangle (see figure 4(c)) will go from f(x) to g(x) and revolve to a shell of incremental volume,
Thus the volume of the bowl is,
Substituting for the functions and integrating gives,
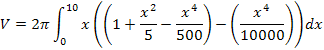
Figure 4(c)
(You may want to maximize your window to see the solution more clearly.)
Any vertical rectangle (see figure 4(c)) will go from f(x) to g(x) and revolve to a shell of incremental volume,
Thus the volume of the bowl is,
Substituting for the functions and integrating gives,
|
Figure 4(c)
|
To find the volume the vase will hold, consider the horizontal rectangles that will revolve to disks along the inside of the vase (see figure 4(d), below).
Figure 4(d)
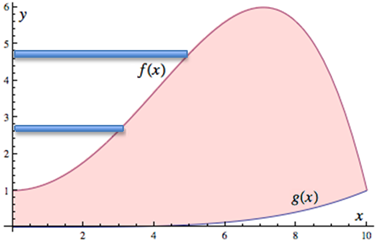
Thus, the interior volume may be found using the disk method along the y‑axis, but to do this, we need the upper limit of integration (the top of the vase). This occurs at the maximum value of (x), which may be found using Calculus I methods (that is, find the derivative of f(x), set equal to zero, and solve). Doing so gives a critical value of 
and a corresponding y value of 6. Thus the volume is given by,
To solve this integral, we need to solve 
for x (actually, x2). Hint: Let u = x2 and solve using the quadratic formula. Thus,
(Note that you can also solve this using shells between y = 6 and y = f(x).)