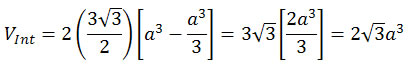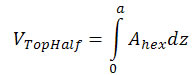
(You may want to maximize your window to see the solution more clearly.)
As with the volume of the intersection of two cylinders, we can use the symmetry of the cylinders to find the volume of the intersection of three cylinders—the volume will be twice the volume of the top half. Here, the intersecting planes (orthogonal to the z-axis) intersect the cylinders in a hexagonal area. So this volume will be the integral of these hexagons of "thickness" dz, that is,
|
To find this area, note that the hexagon can be divided into six equilateral triangles of equal area (see diagram). So the volume is
|
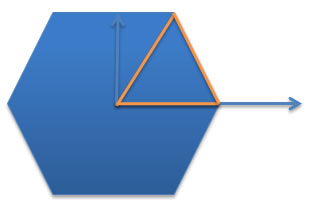 |
The area of a triangle is one-half the base times the height. Because the triangle is equilateral (all sides have the same length), the length of the base is x. The height is perpendicular to the base and forms a right triangle, thus,
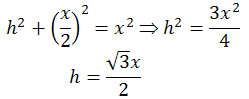 |
And the area of the triangle (as a function of x) is
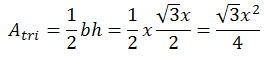 |
This gives the volume (of the top half) as
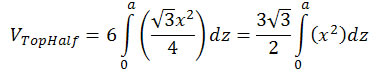 |
Because the integration is with respect to z, we need to find x2 as a function of z. As with the two-cylinder case, a right triangle is formed between the x and z axes and the edge of the cylinder (see the diagram). Again, x2 + z2 = a2, and the volume is

Integrating and doubling the result gives the desired volume of the intersection: