(You may want to maximize your window to see the solution more clearly.)
![]()
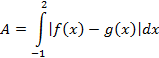
On the interval [−1, 2], we see that g(x) > f(x).
Hint: To check that g(x) > f(x), choose a value in the interval [−1, 2], for example 0. We find that g(0) = 0 and f(0) = −4. Therefore, g(0) > f(0). What does this imply for the entire interval? Because the functions are continuous, it implies that g(x) > f(x) for the entire interval.
Another way to illustrate that g(x) is greater than f(x) over the interval [−1, 2]: Sketch the graphs of f and g on the same coordinate plane and observe that the graph of g(x) is above the graph of f(x) over the interval.
Thus,
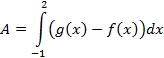
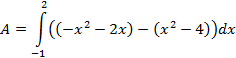
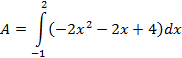
Now, find the antiderivative and evaluate.
![]()

![]()
Hint: If your area came out negative, you have an error.