(You may want to maximize your window to see the solution more clearly.)
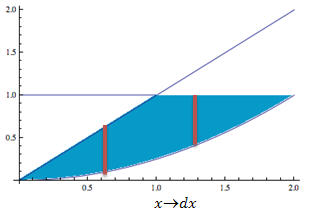
Using vertical rectangles, we would have to consider two different integrals because the upper function is
f(x) = x from 0 to 1, and then changes to an upper function of
![]() from 1
to 2 (see figure 3a).
from 1
to 2 (see figure 3a).
Figure 3a
Using Vertical Rectangles Requires
Two Integrals to Solve for the Area
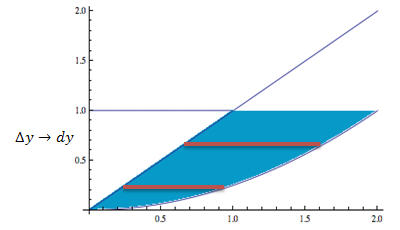
However, if we use horizontal rectangles, they always go from the function
![]() to the function
y = x (see figure 3b).
to the function
y = x (see figure 3b).
Figure 3b
Using Horizontal Rectangles Requires a
Single Integral to Solve for the Area
Now we may set up the integration using horizontal rectangles (of width dy). To do so, we must solve for the functions in terms of y (that is, the inverse functions of f( x) and g(x)).
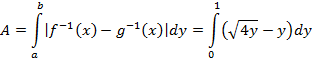
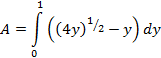
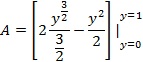
![]()