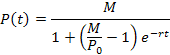
(You may want to maximize your window to see the solution more clearly.)
We want to verify that
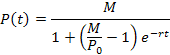
is a solution of the differential equation. But first, we will simplify the notation:
Let ![]()
Therefore,
![]()
Now find the derivative with respect to t,
![]()
![]()
Thus,
![]()
But we also have,
![]()
Simplifying and combining terms with a common denominator gives,
![]()
And finally,
![]()
which is the same as the right-hand side of equation (1); thus,
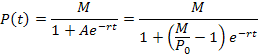
solves the given differential equation.
To examine the asymptotic behavior, we take the limit as time approaches infinity,
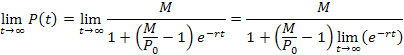
Because M and P0 are constants, only the exponential will be affected by the limit. Because r (the growth constant) is positive, then
![]()
Thus,
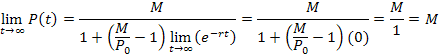
That is as expected (because M is the limiting population value that can be supported by assumption), the population is asymptotic to y = M.