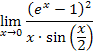
(You may want to maximize your window to see the solution more clearly.)
We want to determine the limit:
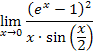
Can we apply l'Hospital's rule? First, let's look at the numerator. We know that
![]()
Therefore,
![]()
Next, we'll look at the denominator:
![]()
We can see that both the numerator and the denominator approach 0 as x approaches 0. Therefore, this rational expression gives us the indeterminate form 0/0, which allows us to use l'Hospital's Rule.
Applying l'Hospital's Rule, we get,
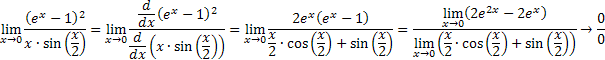
Applying l'Hospital's Rule again, we get
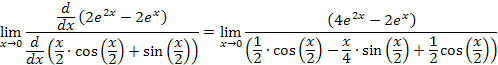
Using the limit theorems (the limit of a sum is the sum of the limits, and so forth), we can evaluate this limit,
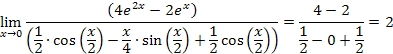
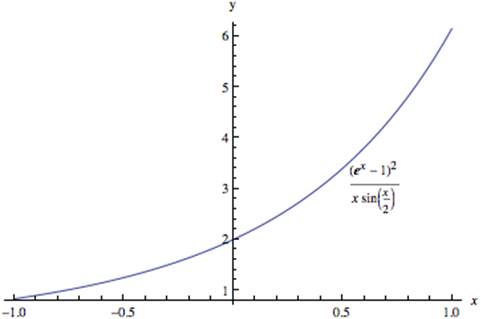
Thus, the limit of the original expression is 2. A graph helps confirm this:
Graph of Curve ![]() near x = 0
near x = 0