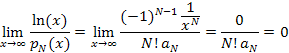be an arbitrary Nth-order polynomial, where aN ≠ 0 (which guarantees the polynomial is Nth order). Thus, 
and because 
, we have the indeterminate form ∞/∞.(You may want to maximize your window to see the solution more clearly.)
Let be an arbitrary Nth-order polynomial, where aN ≠ 0 (which guarantees the polynomial is Nth order). Thus, and because , we have the indeterminate form ∞/∞.
If we apply l'Hospital's Rule repeatedly to the quotient, in each application (until the Nth derivative of the denominator), the denominator will approach infinity because the lead term of pN(x) will contain some power of x. That is, the kth derivative is given by,
.
Thus,
.
But the Nth derivative is a constant,
.
Calculating the derivatives of the numerator gives,
.
Continuing to take derivatives until we reach the Nth order, we have:
.
Hence, applying l'Hospital's Rule to the original expression N times gives,
