,(You may want to maximize your window to see the solution more clearly.)
We see that the limit goes to the indeterminate form of (negative) ∞/∞. Applying l'Hospital's Rule, we get,
,
which is just the limit of the reciprocal of the original expression. Thus, repeated application only continues to "flip" the expression and we never get a form we can evaluate (see Example 4 in the Step-by-Step Explanation section).
Let's try the more conventional method (from Calculus I) of dividing the numerator and denominator by x (or equivalently, multiplying both the numerator and denominator each by 1/x). Because in the limit process (as x → 0), x cannot equal zero, this division is well defined.
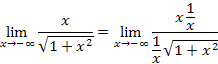
To divide out the denominator term, it is necessary to write x using a square root. But recall that 
, so for the expression to be correct, it is necessary to divide by |x|. That is,
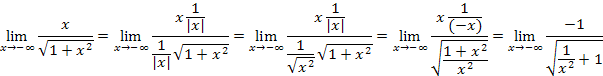
Note that to simplify the numerator, we needed to apply the definition of absolute value. Because we are interested in negative values of x, then |x| = −x.
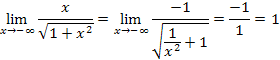
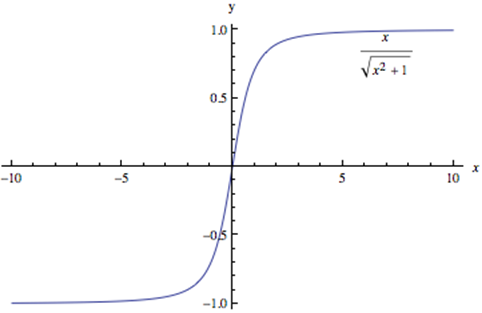
This limit confirms the asymptotic behavior along the negative x‑axis, which we can again confirm with a graph. But remember that a graph is NOT a proof!
Graph of Curve 
