(You may want to maximize your window to see the solution more clearly.)
We want to find the limit:
At first glance, this appears to approach the indeterminate form ∞/∞ raised to the "infinity power"! A closer look shows that we can rewrite the inner expression and get the form,
Now as x → ∞, the term 
approaches zero, so this expression approaches the indeterminate form 1∞. Letting 
and taking the (natural) log of y gives,
Taking the limit of the latter expression as x goes to infinity is the indeterminate form ∞ ⋅ 0, because
,
so we may rewrite it and apply l'Hospital's Rule:
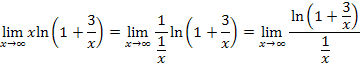
Taking derivatives of the numerator and denominator (be sure to use the Chain Rule!) gives,
Therefore, our original expression (inverting the log to the exponential) goes to e3.
You can also solve this directly if you recognize that
is related to the limit,
.
Using substitution methods, rewrite the limit as
where 
. Applying the basic limit theorems (yes, there are at least two and probably three basic limit properties applied here) gives,
