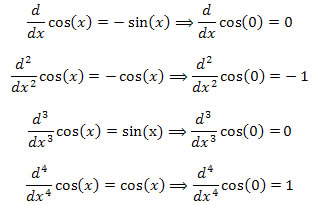
(You may want to maximize your window to see the solution more clearly.)
You can either find the series directly from the derivatives of cos(2x) or find the series for cos(x) and substitute 2x for x. The latter is probably easier.
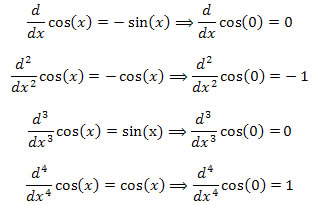
The derivative pattern will repeat, thus,
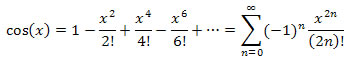
The notation n!, which is read as "n factorial," is by definition, 1 · 2 · 3 · … · n. For example, 4! = 1 · 2 · 3 · 4 = 24.
Writing 2n! (without the parentheses) in the final expression is NOT the same as writing (2n)! . For example, consider

However,
![]()
Therefore, in general, 2n! ≠ (2n)!, so we must be careful when computing factorial expressions.
Thus, we obtain
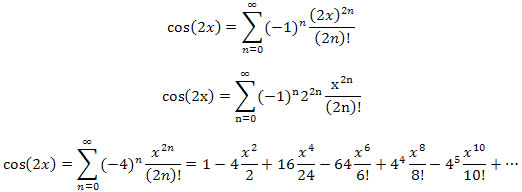
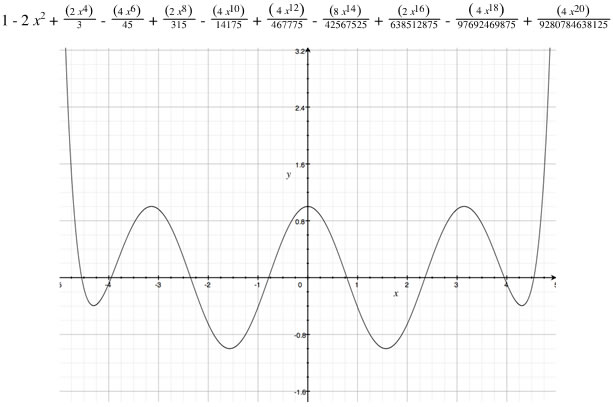
Here is a graph of the 20th-degree polynomial and cos(2x):