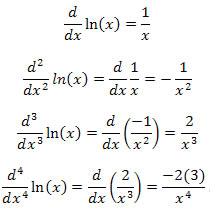
(You may want to maximize your window to see the solution more clearly.)
For the ln(x), note that neither the function nor its derivatives are defined at x = 0, so we want to take the expansion about the point x = 1. Finding the derivatives:
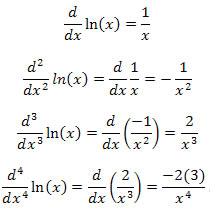
Continuing, we see the pattern:
![]()
Thus, the series is given by
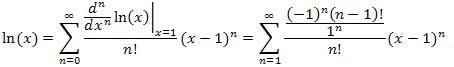
Note that
![]()
Thus, we obtain the result:
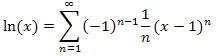
Notice that for the index value n = 0, the term is zero (that is, ln(1) = 0), so this term can be dropped and the sum starts at n = 1.
The Taylor expansion for ln(x + 1) about x = 0 can be found by using the above derivatives and the Chain Rule, noting that ![]()
![]()
Thus, we obtain
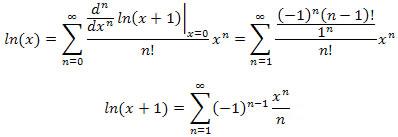
The two series expansions can be shown to be equivalent by replacing x with x – 1 in the above series:
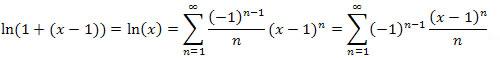
Also, notice that
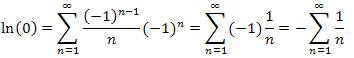
The series
![]()
is known as the harmonic series and does not converge (that is, it "sums" to infinity), which is consistent with the definition of the natural log.