Volumes of Revolution

Archival film of Thomas Edison (Edison, speaking to his intern)

"This is a glass bulb that I have for my new invention—the lightbulb. I need you to measure its volume so I can calibrate the vacuum machine."

We can see from that archival movie footage that Thomas Edison was interested in the volume of that particular bulb because he wanted to calibrate his vacuum machine to take out the air. He didn't know how much air was in there, so he gave his intern the job of finding out the volume.

We'll discuss that more in the Step-by-Step Explanation [section of this topic], where we go over it in detail.

But the important thing to note from that bulb is that it has a circular cross section. That's because the glass blowers had to constantly rotate the bulb to keep heat even on it.

If you look around, you'll notice that a lot of things are that way—as modern machinery developed, the lathe was developed, and so things would rotate and things were manufactured in that way.

So a lot of things have a circular cross section—table legs, glasses, bottles, all kinds of things are now manufactured with a circular cross section.

It's an interesting problem to try to figure out the volume when you are trying to design these different kinds of products.

In calculus, we want to look at how we can calculate [the volume] in advance [of producing the object] and how to use different techniques to do so.

Briefly, in this video, I'm going to cover the main techniques for doing that.

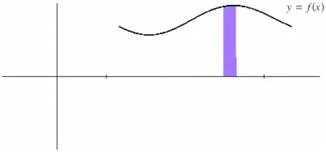
Before talking about volumes, let's make a quick detour back to area. Remember when we were calculating the area under a curve, we drew little rectangles whose widths were dx and whose heights were the value of the function—in this case, the function is the sine of x. We found the area by adding up the areas of all the little rectangles.

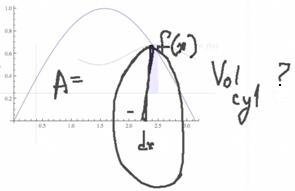
The same thing holds true when doing volume calculations. We want to generate some sort of consistent small volumes and then add them up.

With the volume of revolution, what we'll do is spin this [rectangle] around the axis and get a circular volume—each one of these little rectangles will become a disk, and a disk is just a cylinder. What we'll be interested in is, what is the volume of these individual cylinders?

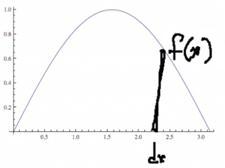
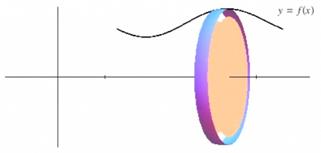
Here is that idea demonstrated by using Mathematica. Suppose we have a curve, y = f(x). Normally, we look at a rectangle [so we can] calculate the area. Here is a typical rectangle.

We're interested in keeping track of how we [draw the rectangle] because the width of the rectangle is set along the x‑axis, and it establishes the limits of the integration variable—the limits of the integration variable would be dx and the height would be the functional value.

And if I rotate the rectangle around the x‑axis …

… you can see that that rectangle becomes a disk.

If we rotate this entire curve [of y = f(x)] around the x‑axis, we are going to get a solid whose cross sections are the disks. If we add up the volumes of all the disks, we get the volume of the cross section. Let's look at how to do that.

If we rotate this entire curve [of y = f(x)] around the x‑axis this time, you can see the rectangle is rotating into a disk …

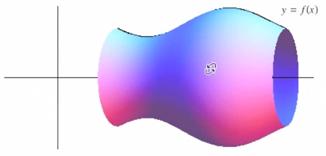
… but the entire curve is rotating into a solid.

We've designed a sort of flower vase or something like that in this particular shape—it's on its side—but we have a nice solid of revolution.

The way to determine its volume is to take all those little disks that were formed from the rectangles revolving around the axis and add them up. As the total number of little disks approaches infinity, the width of the disks gets thinner and thinner, like pancakes or crepes.

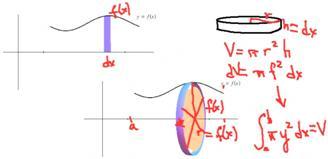
We want to figure out what's the volume of those cylinders, those little disks, and how we add them up to get the limit of integration.

Here we have all the elements we need to deal with. We have a rectangle whose width is dx and whose height is f(x). When we rotate it around, we get a cylinder, or disk, that has thickness dx and whose radius is f(x).

Recall that the volume of a cylinder is πr²h.

When I rotate the rectangle around and get this disk, the radius is simply the distance from the axis out to the function, the f(x) value.

In the cylinder, the height becomes dx and the radius becomes the functional value, so I get an incremental volume of the cylinder of πf ²dx. What we want to do is add up all those little rectangles, and in the limit that's going to be the integral from where you start to where you finish. (Marks a and b on the x‑axis.) The formula for the volume is the integral from a to b of πy²dx.

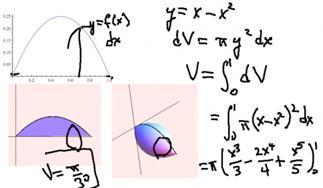
Let's look at an example using y = x – x². That's this parabola with intercepts of 0 and 1. When we rotate it around the x‑axis, we get a football shape.

If we take a rectangle [under the parabola] and rotate it around, it has thickness dx and height y = f(x).

(The author works out the problem, as shown in the screen capture.)

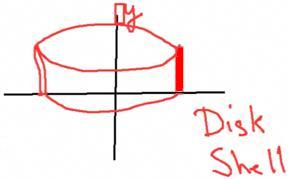
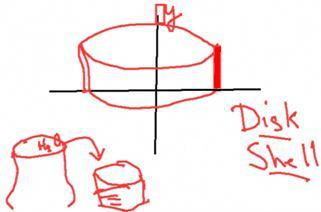
Another method is to rotate [the rectangle] about the y‑axis. If I did, I'd get a shape like a tin can. This is called the shell method, which is covered in more detail in the Step-by-Step Explanation section of this topic.

There is more than one way of doing these volumes of revolution. The two methods are the disk method and the shell method. The disk method is covered in this video. The shell method is covered in the Step-by-Step Explanation section of this topic.

By the way, in solving Edison's problem [of finding the volume of a lightbulb]: Edison was a man of more practical means than theoretical-calculus means. So what he did was fill the bulb with water, pour the water into a graduated cylinder with measurements on the side, and determine the volume that way.

If you have a lightbulb, you can do the same thing by submerging the bulb in water and seeing how much water is displaced.

That doesn't help you if you don't have the bulb or a bucket of water, so the methods of calculus are used a lot more in the design phase of things and in the practical phase of things.

But either way, it's nice to have these ways of determining volumes.

(Edison, pouring water obtained from the lightbulb into a graduated cylinder to determine the volume)