Volumes of Revolution
Introduction
Around 278 BCE, King Hiero II of Greece (as the story goes) had a crown made of pure gold but suspected that the goldsmith had cheated him by mixing silver with the gold. He asked a young, brilliant mathematician named Archimedes to determine, without damaging the crown, whether it was pure gold. While taking a bath and pondering this problem, Archimedes had a "eureka moment" that gave him the solution (Vitruvius, ca. 15 BCE).
Archimedes realized that the volume (weight) of water displaced by an object is equal to the volume of the object itself. This principle, now named for him, helped Archimedes establish that the crown was indeed not pure gold and that the goldsmith was in a lot of trouble. Archimedes's Principle has led to many applications, including the Falkirk Wheel in Scotland.
Archimedes's Principle is an interesting way to determine volumes, but it is effective only if you have the object. In many cases, particularly in the design phase of manufacturing, it is necessary to find the volume of an object that does not yet exist. This is where calculus becomes a valuable tool.
Although the use of calculus in determining volumes can be quite involved (for example, see the Steinmetz intersection of cylinders topic), there are some special cases that have wide application. One of these is the calculation of volumes of revolution. In fact, many manufacturing methods involve a rotation about an axis of symmetry. For example, machining or turning on a lathe produces objects of circular cross section, and these methods are generalized in many production methods—those used to create bottles, table legs, and baseball bats are good examples.
There are two primary methods for finding volumes of revolution, which we briefly introduce here and cover in detail in other sections of this topic. These methods are the disk method and the shell method.
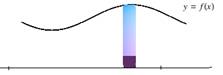
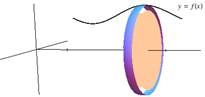
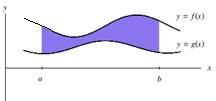
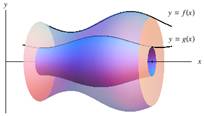
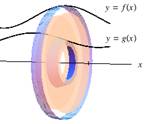
When an area is rotated about an axis (x‑axis, y‑axis, or a line), the rectangles that approximate that area will trace out a disk or washer, as shown below in figures 1 and 2, or a shell (cylinder), as shown in figure 3. As in calculating areas, it helps to visualize the approximating rectangles of the area and the resulting shape when rotated about an axis. These rectangles will sweep out disks or shells that can be used to set up the corresponding integrals to find the volumes of revolution.
Figure 1
Disk Method: Tracing Out a Disk
(a) |
(b) |
|
|
Figure 2
Disk Method: Tracing Out a Washer
(a) |
(b) |
(c) |
|||
|
|
|
Figure 3
Volume Generated by Shell Method
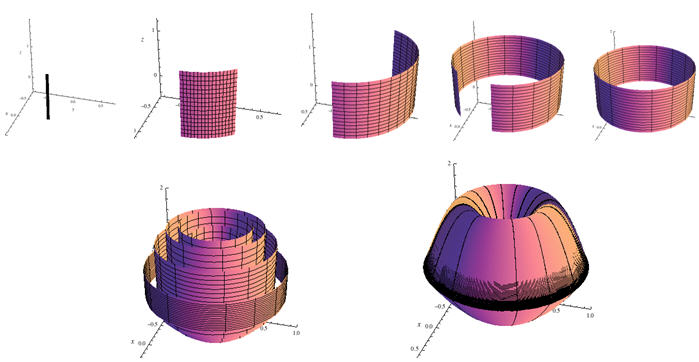
For a given volume of revolution, either the disk or shell method should work to provide the correct answer, although in some cases one or the other may be easier to calculate (see the Summary section for an example that explains which method to use). We will describe the disk and shell methods in detail in the video and other sections of this topic.
Reference
Vitruvius, M. (ca. 15 BCE). De architectura (book 9, paragraphs 9–12). Available from http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Vitruvius/9*.html. (Based on Gwilt, J. (Trans.). (1826). The architecture of Marcus Vitruvius Pollio. London, England: Priestley & Weale.)