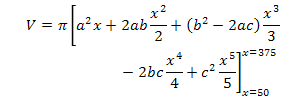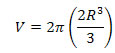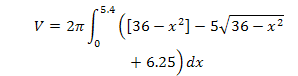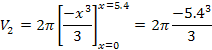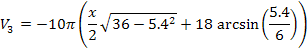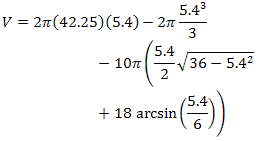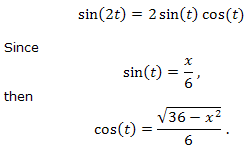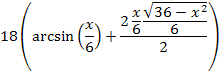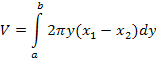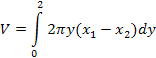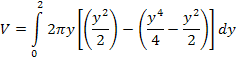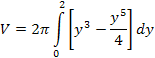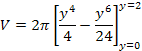Volumes of Revolution
Step-by-Step Explanation
Example 1: Find the volume of Edison's lightbulb.
Example 2: Derive the formula for the volume of a sphere.
Example 3: Determine the (average) volume of an NRL/NCAA football.
Example 4: Determine a volume generated by revolving the area between two functions.
Example 1
| Figure | Problem | |
|---|---|---|
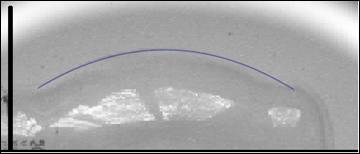
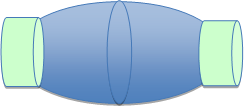
Scanning the photo of the bulb, it can be modeled with the two ends as cylinders of radius 85 (pixels) and length 50 (pixels). The center section may be modeled as the parabolic arc, y = 46.459 + 0.7959 − 0.001889 x2 rotated about the x‑axis on the interval [50, 375] (pixels). (Note that the scanning resolution is 150 pixels to one inch. Thus, pixel units will be used for the problem with a conversion once the volume is determined in cubic pixels.) |
Find the volume of Edison's lightbulb (as seen in the Video Lecture).
|
|
| Step | Equation | Explanation |
1 |
We model the top half of the bulb as the piecewise function
|
To model the bulb, we used software to select points along the top curve of the image of the bulb. A polynomial curve was then fitted to these points (see methods of least square). [We used Mathematica to fit the curve, but many other software packages (for example, Geometer's Sketchpad) can accomplish the same thing. Also, the numbers here are not exact; they were rounded to make the calculations more convenient.] |
2 |
To set up the calculation, let a = 46.46 |
Define some constants to help write the equations. |
3 |
|
The two ends of the bulb are considered to be cylinders, each with volume V = πr2 h = π802(50) = 320000π. Thus, their combined volume is 640000π. |
4 |
|
The volume of the center section may be found using the disk method of integration on the interval [50, 375]. |
5 |
|
Substituting for y and expanding gives a polynomial (in terms of a, b, and c). |
6 |
|
Integrating term by term gives the expression at left. |
7 |
V = π (4.27223 × 106) = 1.34216 × 107 |
Substituting for a, b, and c where a = 46.46 and evaluating for x gives the volume (in pixel units). |
8 |
|
Here, we convert to cubic inches for the center section. |
9 |
|
Converting the volume of the two ends (see Step 3) into cubic inches gives the value at left. |
10 |
|
Adding the pieces (ends, shown in green, plus the center section, shown in blue) together gives our approximation of the volume. |
Example 2
| Figure | Problem | ||
|---|---|---|---|
|
Derive the formula for the volume of a sphere. |
||
| Step | Equation | Explanation | |
1 |
|
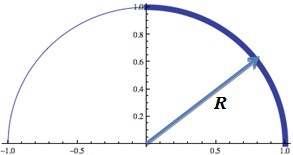
A sphere may be generated by revolving a semicircle around the x‑axis (by symmetry, it could be either coordinate axis). |
|
2 |
|
Again, using symmetry, the quarter-circle in the first quadrant can be rotated about the x‑axis and the resulting volume doubled. Suppose the sphere (and thus, the circle) has radius R, as shown. |
|
3 |
x2 + y2 = R2. |
The equation of the circle of radius R, centered at the origin, is given at left. |
|
4 |
|
The volume is given by the equation at left (remember that the factor of 2 is from doubling the volume of the hemisphere generated from the quarter-circle). |
|
5 |
|
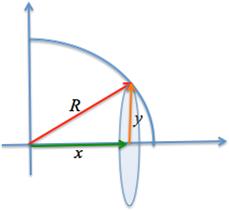
The radius (red line), x‑coordinate (green line), and y‑coordinate (orange line) for a right triangle whose y leg is the radius of the disk is shown at left. Thus, x2 + y2 = R2.
Solving for y2 and substituting gives the integral of the volume given at left. |
|
6 |
|
Here, we integrate term by term. |
|
7 |
|
Here, we evaluate for x. |
|
8 |
|
Simplifying. |
|
9 |
|
Multiplying gives our result in cubic units. |
|
Example 3
| Figure | Problem | ||||
|---|---|---|---|---|---|
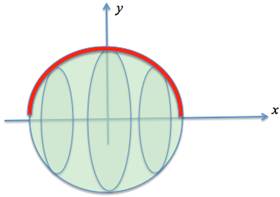
A vesica piscis is the intersection of two identical circles.
|
Determine the (average) volume of an NRL/NCAA (National Rugby League/National Collegiate Athletic Association) football.
|
||||
| Step | Equation | Explanation | |||
1 |
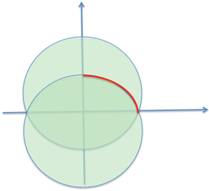
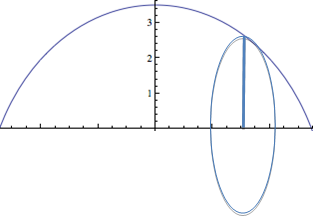
The NRL/NCAA football can be modeled as a vesica piscis.
x2 + (y ± 2.5)2 = 62 |
An official football (the NRL and NCAA balls have the same dimensions) has a length of 11 inches and a center circumference of 22 inches (thus, a center diameter of approximately 7 inches). The area to be rotated (shown at left) can be modeled as a pair of intersecting identical circles (a vesica piscis) with a radius of 6 and an offset on the y‑axis of 2.5 inches. By symmetry, we need only rotate about the x‑axis the arc (shown in bold red, below) lying above the x‑axis of the bottom circle.
|
|||
2 |
|
The disk cross sections have radii that are the function value from the x‑axis to the circle; that is,
|
|||
3 |
|
The x‑intercept is approximately x = 5.45, but because the ends are "flattened," let's use x = 5.4. |
|||
4 |
|
Solving the equation of the circle for y gives the function at left. |
|||
5 |
|
Here, we substitute y into the volume integral. |
|||
6 |
|
Expand the quadratic. |
|||
7 |
|
Simplify by combining the constant terms. |
|||
8 |
V = V1 + V2 + V3 |
The integral has three terms (V1, V2, and V3), as defined in Steps 9, 10, and 11. |
|||
9a |
|
V1: The integral of the constant term is shown at left. |
|||
9b |
|
Integrating gives the first part of the integral. |
|||
10a |
|
V2: Second, integrate the quadratic term. |
|||
10b |
|
Evaluating, we have the second term. |
|||
11a |
|
V3: Last, integrate the square root term. This integral has a more difficult antiderivative, detailed in steps 11b and 11c. |
|||
11b |
|
From integral tables (or a symbolic algebra like Mathematica), we can determine the necessary antiderivative. (We also derive it below in steps A–F.) |
|||
11c |
|
Evaluating gives the expression at left. (Note that the arcsin(0) = 0.) This gives us the value of the third term. |
|||
12 |
|
Combine V1, V2, and V3 to find our volume. |
|||
13 |
V ≈ 248.66 (cubic inches) |
Evaluating with a calculator gives our approximation. |
|||
| Derivation of the Antiderivative in Step 11b | |||||
A |
|
This integral may be found using the methods of trigonometric substitution. |
|||
B |
|
Let x = 6 sin(t), then dx = 6 cos(t) dt. Substituting gives the integral at left. |
|||
C |
|
Using the trig identity, sin2(t) + cos2(t) = 1. |
|||
D |
|
To solve this integral, use the trig identity,
which is sometimes called the Half-Angle Formula. |
|||
E |
|
Integrating term by term gives the expression at left (plus an additive constant). |
|||
F |
|
The expression needs to be converted to a function of x. We know that 6 sin (t) = x, but our expression is in terms of 2t! Once again, we use a trig identity. |
|||
G |
|
|
|||
H |
|
Substituting and simplifying gives the antiderivative (up to an additive constant) used in Step 11b. |
|||
Example 4
| Figure | Problem | |
|---|---|---|
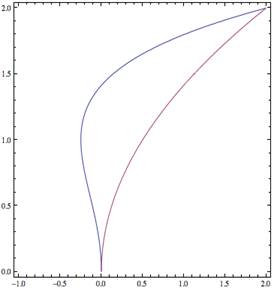
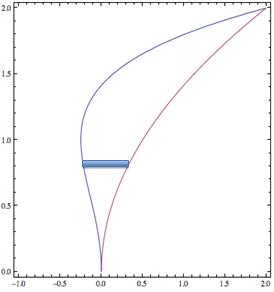
|
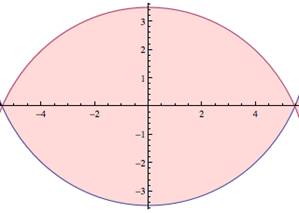
Determine a volume generated by revolving the area between
and
about the x‑axis (see the graph). |
|
| Step | Equation | Explanation |
1 |
|
It is easiest to find the area trapped between the curves by using a horizontal rectangle, because it will always go from one curve to the other. Revolving this horizontal rectangle about the x‑axis will result in a shell; thus, we use the shell method to find the volume. |
2 |
|
The shells will have radius y, thus their circumference is 2πy. Their width is along the y‑axis, so is Δy, which becomes dy in the integral. Finally, the shells have their "heights" along the x‑axis; the height is
|
3 |
|
Because the curves intersect at (0, 0) and (2, 2), then a = 0 and b = 2 (along the y‑axis). |
4 |
|
Substituting for the x terms and simplifying results in our integral. |
5 |
|
The integral can be evaluated term by term. |
6 |
|
Evaluating gives our result (in square units). |