Volumes of Revolution

Summary

Revolving an area (region of the xy plane) about an axis is a method often used to generate a volume. Because it involves fairly straightforward principles in calculus, designers, engineers, and manufacturers are interested in this approach to finding volumes. Calculus provides two commonly used methods for computing volumes of rotation: the disk method and the shell method. We will also discuss the washer method, which is related to the disk method.

The Disk Method

Recall that when calculating the area under the curve of a function f(x), the area on the interval [a, b] is the integral that is the limit of the sum of approximating rectangles. If this area under the function on this interval is rotated about the x‑axis, the area forms a volume of revolution and the rectangles form disks in this volume (see figure 1). Just as the area can be found as the limit of the sum of the areas of the rectangles, the volume can be determined by the limit of the sum of the volumes of these disks. This volume is the integral given as:

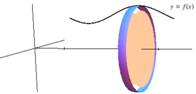
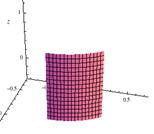
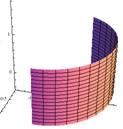
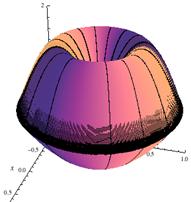
In figure 1 below, we can see that rotating the function y = f(x) about the x‑axis [1(a)] results in a volume of revolution [1(b)] whose cross section [1(c)] is circular. Notice that rectangles used to approximate the area under the curve revolve to become disks that may be used to approximate this volume of revolution.

Figure 1
Calculating Volumes of Revolution
Using the Disk Method

(a) Rotating y = f(x) About the x-Axis	(b) Volume of Revolution	(c) Circular Cross Section

This integral is derived as follows. The volume can be approximated, as noted, by the disks of revolution. These disks are really flat cylinders whose "height" is the distance Δx along the x‑axis and whose radius is the distance from the x‑axis to the surface of revolution, which is just the distance y = f(x). Because the volume of a cylinder is V_cyl = πr²h, the volume of each approximating disk is V_disk = ΔV = πy²Δx. Summing these approximations and taking limits results in the volume formula.

The Disk Method

Let f(x) be a (continuous) function that is rotated about the x‑axis on the interval [a, b] to form a volume of revolution. The volume of this solid is given by,

An analogous result can be formulated for rotations about the y‑axis.

The Washer Method

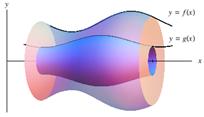
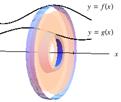
A volume of revolution can also be generated analogously to calculating the "area between two curves." In figure 2 below, we can see that rotating an area [2(a)] trapped between two functions about the x‑axis results in a volume of revolution [2(b)] whose cross section is a "washer" (that is, a disk with a hole), as shown in 2(c). This leads to a method similar to the disk method called the washer method.

Figure 2
Calculating Volumes of Revolution Using the Disk Method
(Rotating an Area Between Two Functions)

(a) Rotation of Area Between Two Functions	(b) Volume of Revolution	(c) "Washer" Cross Section

As one might guess, the formula for the resulting volume using the washer method is equivalent to the "outer volume" minus the "inner volume" and is given by:

This volume may be calculated as a single integral or as two integrals—whichever is most convenient. Note that the order of the function is important here. Although each term is positive, the difference may not be, unless the inner function is subtracted from the outer function. If you end up with a negative volume, these terms are probably reversed.

The Shell Method

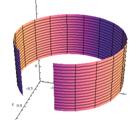
If we rotate the rectangle in figure 1 about the y‑axis instead of the x‑axis, it forms a "can-like" shell (see figure 3). As with the disk method, these shells can be used to build and approximate a volume (see figure 4). To calculate the volume, we must determine the volume of each shell.

Figure 3
Rotating a Rectangle About a Vertical Axis
Results in a "Can-Like" Shell

image showing the rectangle that will be rotated about the vertical axis to form a can-like shell

image showing the beginning of the formation of a can-like shell resulting from a rectangle being rotated about the vertical axis

image showing further formation of a can-like shell resulting from a rectangle being rotated about the vertical axis

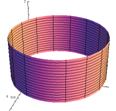
image showing the formation of a can-like shell resulting from a rectangle being rotated about the vertical axis

Figure 4
Volume Generated by Shells

image showing the stacking of can-like shells to begin to form a volume of revolution

image showing further stacking of can-like shells to begin to form a volume of revolution

image showing the volume generated by stacking can-like shells

A closer examination shows that each shell can be "unrolled" to a rectangular solid of thickness dx, with the length equal to the circumference of the shell, and the height equal to f(x) (see figure 5).

Figure 5
Volume of a Shell

Each shell can be unrolled to a rectangular solid of thickness dx, with the length equal to the circumference of the shell, and the height equal to f(x).

(Incremental cylindrical volume: ΔV_i = C_i h_i Δx = 2πx_i* f(x_i* )Δx)

Thus, V_shell = ΔV = 2πxf(x)Δx.

Formalizing this procedure with limits results in the integral formula.

The Shell Method

Suppose an area under the curve y = f(x) is rotated about the y‑axis on the interval [a, b], then the resulting volume is given by the shell method as,

An analogous result holds for a rotation about the x-axis.

See the Step-by-Step Explanation section for a demonstration of the shell method.

The volume of a shell is equivalent to a rectangular solid of length equal to the circumference of the shell, height equal to the function value, and thickness equal to the width of the subintervals (Δx). Because , then .

Which Method Is "Better"?

Both the disk and shell methods will give you the correct answer for a given problem. So … is one "better" than the other for calculating volume? Although there may not be a better method because both should generate the correct answer, a proper choice can make the calculations a bit easier. To make this choice, we can refer back to calculating areas. Consider the following example.

Suppose the area (see figure 6) between the parabola (y − 1)² = x and the line y = x − 1 is rotated about the x‑axis.

Figure 6
Rectangles Generating the Disk Method

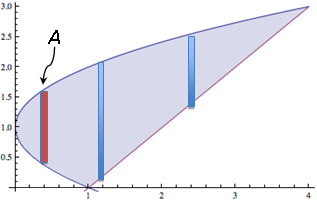
vertical rectangles placed between the parabola (y − 1)^2 = x and the line y = x − 1

(Notice that the red rectangle "A" goes from
one part of the parabola to another part of the same parabola.)

Using "vertical" rectangles to approximate this area would result in "washers" in the volume. Note, however, that some of these rectangles (for example, the red vertical rectangle "A" in figure 6) run from one part of the parabola to another part of the same parabola. This calculation would require breaking the parabola into its two implied functions of x, as well as breaking the interval of integration ([0, 4]) into two parts ([0, 1] and [1, 4]). Thus, the volume would be given by,

However, if we use horizontal rectangles, as shown in figure 7, any approximating rectangle would always go from the line to the parabola.

Figure 7
Rectangles Generating the Shell Method

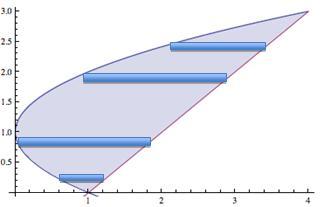
horizontal rectangles placed between the parabola (y − 1)^2 = x and the line y = x − 1

(Note that ALL the rectangles used to generate the
shell method go from one curve to the other.)

Rotating these rectangles about the x‑axis gives the shell method with volume,

Note that the volume integral is now over y and the integrand is a polynomial in y and thus is easy to integrate. Note also that there is only one integral rather than two.

You can see that using vertical rectangles resulted in a more complex volume calculation than using horizontal rectangles, so the shell method would be the better, or easier, method to use in this case.

Return to top.