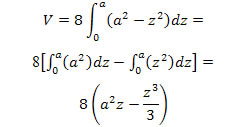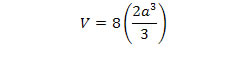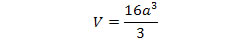Steinmetz Intersection of Cylinders—The Perpendicular Intersection of Two Identical Cylinders

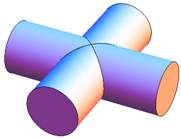
The problem is to determine the volume contained in the intersection (that is, the volume in common) of two identical cylinders, each of radius a, whose axes intersect at right angles (that is, orthogonally).

1

In general, a volume is determined by integrating small volumes (dV) that are areas of "thickness" dz. Here, the integral will run from the bottom of the cylinders (z = −a) to the top (z = a).

2

Using the symmetry of the cylinder (the top half is identical to the bottom half), the integral can be evaluated by integrating from z = 0 to z = a, and then doubling the result.

Here is a three-dimensional visualization of the intersection inside the cylinders. Cutting a slice through the volume (perpendicular to the z-axis) results in an area that is a square.

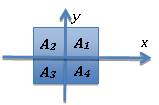
Using the symmetry of the cross-sectional square about the axes, it can be subdivided into four identical squares, each with the same area.

3

Thus, the area of the (cross section) square A(z) can be written as 4 times the area of one of the smaller squares. So that our coordinate values are positive, take the square A₁ in the first quadrant.

4

The area of A₁ is the length x along that axis times the length y along that axis. But because the (rectangular) area is a square, the values of x and y are equal. Choosing to use x, the area can be written as A₁ = x².

5

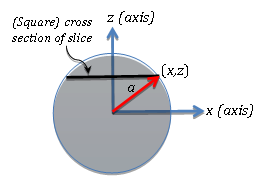
Because the "thickness" dz is along the z-axis, the integration is with respect to the z variable. Thus, A₁ must be written as a function of z. In this case, the Pythagorean Theorem gives:

x² = a² − z²

Note that a is constant because it is the radius of the cylinders.

6

Because the previous step is a bit tricky, let's consider it in more detail.

Slicing across the cylinders, as seen above, results in a square cross section. Viewed from the end of one of the cylinders, this square slice will appear as a line segment (black) across the z-axis to the edges of the cylinder. The point on the cylinder has coordinates (x, z). Running a line from the origin to this point (the red line) forms a right triangle with legs of length x and z, and a hypotenuse of length a (because it is the radius of the cylinder!). The Pythagorean Theorem states that the sum of the squares of the legs equals the square of the length of the hypotenuse. Thus,

z² + x² = a²

Solving for x² gives

x² = a² − z²

7

Because the integral of a sum is the sum of the integrals, each piece can be integrated separately. Finding the antiderivative of each function gives the next step.

8

These antiderivatives are evaluated at the limits of integration.

9

Because the evaluation at z = 0 is 0, only terms of a are left.

10

Subtracting (the fractions) gives an expression for the volume in terms of the radius a.

11

Multiplying by 8 gives the total volume of the intersection.