Steinmetz Intersection of Cylinders—The Perpendicular Intersection of Two Identical Cylinders

Summary

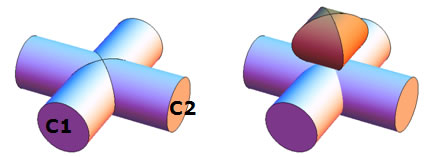
Let C1 and C2 be two right cylinders of the same radius R = a. If the cylinders intersect axes at a right angle (see representation), what is the volume common to both cylinders? That is, what is the volume in the intersection?

Figure 1
The Perpendicular Intersection of Two Identical Cylinders

two intersecting cylinders and the volume of intersection being lifted out

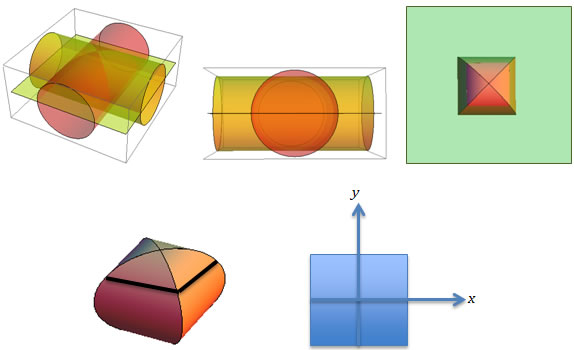
This problem is similar to volume-of-revolution problems, except that here, the "slices" are not disks, but squares. (See the video for details.) Furthermore, by symmetry, the top and bottom "halves" are identical, and each "square slice" is symmetrical about both axes, so it is made up of four smaller, identical squares. The diagrams below show the slices from various angles, demonstrating (1) the symmetry of the cylinders, and (2) that the slices are actually squares.

Figure 2
Various Views Showing the Symmetry of the Cylinders
and the Square Cross Section

symmetry of the top and bottom halves of a cylinder, view from the top showing that the intersection is a square, and the square divided into four quadrants

Thus, the volume is 8 times the volume in the first quadrant. Hence, the volume is given by:

where dV is the differential volume of the rectangular parallelepiped equal to A(z)dz, where dz is the "thickness" and A(z) is the area of the first quadrant square in the intersection slice. Thus, A can be found from the area of the x‑y square in the first quadrant, which is A = xy = x² = y². Thus,

Here, the Pythagorean Theorem was used to determine x² = a² − z² (see diagrams below).

Figure 3
Using the Pythagorean Theorem to
Calculate x for the Area of the Square

right triangle in the volume intersection formed by the z axis, the x axis, and the radius of the cylinder

Integrating gives,

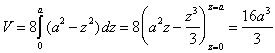
Thus, the volume of the intersection is the radius of the cylinders cubed, times .

Return to top.