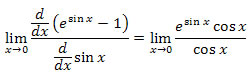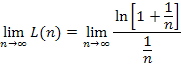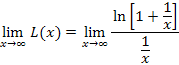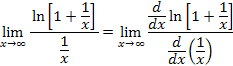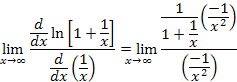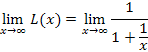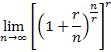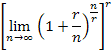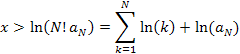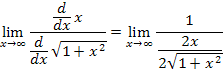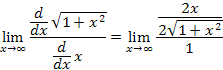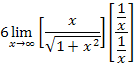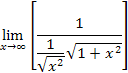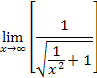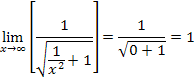L'Hospital's Rule
Step-By-Step Explanation
Example 1
| Figure | Problem | |
|---|---|---|
|
Find the limit:
|
|
| Step | Equation | Explanation |
1 |
|
Because both the sine function sin x and exponential function ex are continuous, we can move the limit symbol through the exponential and sine functions. In other words, because ex and sin x are both continuous at x = 0, we can simply plug in x = 0 to find the limit. Therefore, the numerator approaches 0. Similarly, the denominator approaches 0. So the limit is in the indeterminate form 0/0, which means we may use l'Hospital's Rule. |
2 |
|
Applying l'Hospital's Rule gives a rational expression that can be evaluated. |
3 |
|
The cos x terms divide out (because they are not zero near x = 0), and we can evaluate the limit. |
4 |
|
Thus, the limit we seek is 1. |
5 |
|
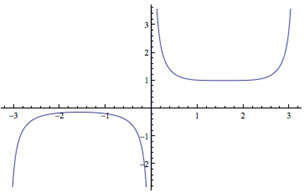
Some of you may be tempted to think that the value of 1 is the y intercept in the opening figure, but that is incorrect. Our rational function is not defined at x = 0 (its graph is shown at left). In fact, you may now recognize that this rational function represents the derivative of esin(x) at x = 0. Thus, the tangent line to esin(x) at x = 0 has slope 1. WAIT! Weren't we warned in the Introduction not to use l'Hospital's Rule to evaluate derivative expressions? |
6 |
|
That's true if the derivative you use in the evaluation is the derivative you are trying to evaluate. Here, the derivatives of sin x and ex are derived independently of esin x, which also requires the Chain Rule (which has also been derived independently of our use of l'Hospital's rule). The graph at left shows the function esin x along with the tangent line (of slope 1) at x = 0. |
Example 2
| Problem | ||
|---|---|---|
Show that,
|
||
| Step | Equation | Explanation |
1 |
Let |
First, let's let r = 1 (rate of 100%) and show,
|
2 |
|
Define some functions of n to make the notation easier. Note that because ln(1) = 0,
By using the reciprocal of n, the limit is converted to the indeterminate form 0/0. |
3 |
|
The limit on L(n) as n → 0 is the indeterminate form ∞ ⋅ 0, since |
4 |
|
Rewrite the expression using the reciprocal of n. The limit now has the indeterminate form 0/0. |
5 |
|
The limit in n (a discrete variable) is the same as the limit in x (a continuous variable). |
6 |
|
Apply l'Hospital's Rule by taking the derivatives of the numerator and denominator. |
7 |
|
We can divide out the terms |
8 |
|
The limit is now well-defined because |
9 |
|
Knowing the limit on L(x) can be used to find the limit on A(x). |
10 |
Because
|
Rewrite, using the properties of logarithms and exponential functions. |
11 |
|
Using the substitution rule for limits of continuous functions, we can determine the limit for A(x). |
12 |
|
Applying our result on the limit of L(x) gives our result. |
13 |
Show |
We now return to our original limit problem. |
14 |
|
Rewrite the limit expression using the law of exponents. |
15 |
|
Because the limit does not depend on r, we can take the limit inside the exponential expression. |
16 |
|
Let |
17 |
The
|
Use our previous result to take the limit. |
Example 3
| Figure | Problem | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
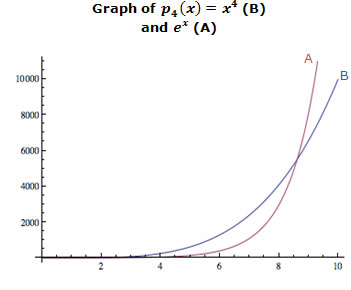
Although p4(x) is greater at first, the exponential function eventually becomes greater for x > 9. |
Show that,
for any Nth‑order polynomial pN(x). That is, exponential growth is eventually faster than any polynomial growth. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| Step | Equation | Explanation | ||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
Define pN(x) as an arbitrary Nth‑degree polynomial, that is, aN ≠ 0. |
||||||||||||||||||||||||||||||||||||||||||||||||
2 |
Continuing …
|
Examine the derivatives of pN(x). Note that the Nth derivative of pN(x) is a constant, whereas the lower-order derivatives depend on x (because aN ≠ 0, the leading term of the derivative will always depend on a power of x). |
||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
Now let's consider our limit and apply l'Hospital's Rule. |
||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
A repeated application of l'Hospital's Rule reduces the degree of the numerator, but we still have an indeterminate form. |
||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
Because |
||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
But the Nth derivative (application of l'Hospital's Rule) results in a constant nonzero numerator term (thus, we can no longer apply l'Hospital's Rule). |
||||||||||||||||||||||||||||||||||||||||||||||||
7 |
|
Although N! can be extremely large (try calculating 70! on your calculator), eventually, ex is larger. |
||||||||||||||||||||||||||||||||||||||||||||||||
8 |
|
In fact, using the properties of the logarithm, we can see that even for moderately large x, the exponential is quite large. |
||||||||||||||||||||||||||||||||||||||||||||||||
9 |
|
The table at left shows that for x > 365 plus the ln(aN), the exponential will start growing faster than a 100th-degree polynomial. Similar estimates can be calculated for higher-order polynomials, but the exponential will always grow faster eventually. |
||||||||||||||||||||||||||||||||||||||||||||||||
10 |
|
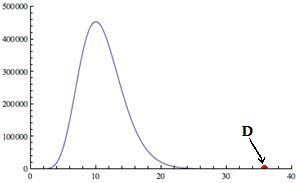
The graph at left is of the ratio
The red dot (D) shows where the ratio becomes 1; that is, ex intersects and overtakes x10 (at x approximately 35.7715). Notice the y-axis scale and how the polynomial growth dominates for x < 10 but then starts to fall behind the exponential growth, eventually losing out as the ratio goes to zero. |
||||||||||||||||||||||||||||||||||||||||||||||||
Example 4
| Figure | Problem | |
|---|---|---|
|
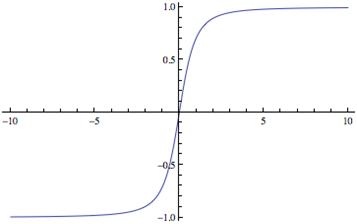
Find the (asymptotic) limit:
|
|
| Step | Equation | Explanation |
1 |
|
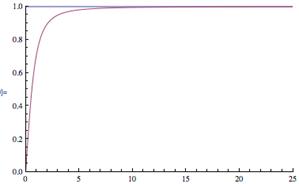
The limit is of the indeterminate form ∞/∞, but the graph, shown above left, indicates that the function may level off to an asymptote. |
2 |
|
Apply l'Hospital's Rule. |
3 |
|
Simplifying gives a result that is the reciprocal of our original rational expression and still has an indeterminate form. So let's apply l'Hospital's Rule again. |
4 |
|
Taking the derivatives and simplifying, we see that the result is our original rational expression! Thus, if we continue to apply l'Hospital's Rule, the results will just keep repeating and will always be indeterminate forms. Thus, l'Hospital's Rule fails in this case! |
5 |
|
Because the graph does indicate a limit (asymptotic behavior), let's try another method from Calculus I. Multiply the numerator and denominator by |
6 |
|
In order to move the x inside the square root, it is rewritten as |
7 |
|
Because |
8 |
|
The graph at left shows the horizontal asymptote at y = 1 as derived from our limit calculations. |
| Lesson | ||
Do not blindly apply l'Hospital's Rule to an indeterminate limit—examine it first to see if the indeterminate form may be solved with standard limit procedures. A graph can help, but remember that a graph is not a proof of the actual limit value. |
||