L'Hospital's Rule
Introduction
L'Hôpital's Rule, alternatively known as l'Hospital's Rule (with a silent s), is a calculation tool used in calculus to find the limits of "indeterminate forms"—that is, limits that approach the rational forms 0/0 or ∞/∞. There are also other "indeterminate forms," which we will discuss below. Exactly what are these indeterminate forms, and why do we care to know how to find their limits?
Indeterminate forms occur most commonly in the limits of rational functions—that is, functions that are the quotient of two functions, where the numerator and denominator both approach zero or infinity. Indeterminate forms can also occur in limits that approach expressions such as 00, 1∞, and so forth. Recall from Calculus I that the limit of a quotient is the quotient of the limits; that is, for a rational function 
,
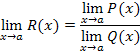
If the limits 
and 
both exist and 
is not 0, there is no problem applying this quotient rule. (NOTE: Saying that a limit exists is implying that it is finite and hence not infinite.) In the case where both limits approach zero or both approach infinity, however, we have an indeterminate form.
Thus, an indeterminate form occurs when the limits go to 0/0 or ±∞/±∞. The forms 0/±∞ and ±∞/0 are not indeterminate because the former limit is zero and the latter is "infinite."
Indeterminate forms can also be applied to products of functions that result in a form like 0 ⋅ ∞ because these can be written as an indeterminate form of a quotient. We will consider only indeterminate forms of quotients.
Consider the following example:
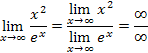
The limit appears to be indeterminate, but a plot of the rational function indicates that the limit (horizontal asymptote) might exist and be zero. For example, look at the rational function 
.
Figure 1
Graph of the Rational Function 
(Notice the behavior for x > 10.)
A table of values indicates the same behavior.
| x value | R(x) value |
|---|---|
| 5 | 1.68E-01 |
| 10 | 4.54E-03 |
| 15 | 6.88E-05 |
| 20 | 8.24E-07 |
| 25 | 8.68E-09 |
| 30 | 8.42E-11 |
| 35 | 7.72E-13 |
| 40 | 6.80E-15 |
As the x values increase, the R(x) values decrease in a way that the limit appears to be zero. Of course, neither a graph nor a finite table of values is a proof of the actual asymptotic behavior.
This is the type of problem that l'Hospital's Rule addresses. L'Hospital showed that when the limit is an indeterminate form of a rational function, the limit can be found from the quotient of the derivatives of the numerator and denominator. Formally stated:
L'Hospital's Rule
Let 
be a rational function where P(a) = Q(a) = 0 and both of these functions are differentiable on some interval I containing x = a; then,
assuming these latter (right side) limits exist. If this limit is 0/0 as before, this process may be continued (assuming the higher-order derivatives exist) until either the numerator or denominator is nonzero. Note, however, that this rule does not apply whenever the numerator or denominator has a nonzero (finite) limit. The rule does apply if the indeterminate form is ∞/∞ and if a approaches ∞.
Applying l'Hospital's Rule to our example above gives,
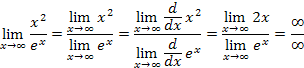
Because the result is still indeterminate, apply l'Hospital's Rule again and obtain,
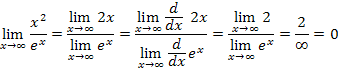
That is, the numerator limit goes to a finite value, 2, while the denominator grows large; thus, the overall limit of the quotient is zero.
This example shows that the exponential function grows asymptotically faster than x2. In fact, exponential growth is asymptotically faster than any polynomial growth. That is,
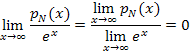
for any Nth-order polynomial pN(x). This can be shown by repeatedly applying l'Hospital's Rule. Complete details are provided in the Step-by-Step Examples section of this topic.
An application of these ideas may be found in the calculation of compound interest. Compound interest gives a better yield than simple interest because it is, in a sense, exponential; but what is the asymptotic behavior as the number of compounding periods increases? That is, do your returns go infinite (!) as the number of compounding periods goes to infinity? (The result is called continuously compounding.)
Recall that the compound interest formula for one monetary unit (which may be one dollar or one billion dollars) over one year is given by,
Where n is the number of compounding periods, A(n) is the amount of principle (in terms of the monetary unit) after one year, and r is the annual interest rate. We want to determine the behavior as n goes to infinity; that is,
Notice that the exponent n should make the limit grow exponentially, but that the effective interest rate (per compounding period) n/r is going to zero. As the problem stands, we cannot apply l'Hospital's Rule; but because the (natural) log is continuous, we can consider ln(A(n)) to determine the limit. This will give us (see the Step-by-Step Examples section for details),
(Remember that our time period is one year. For t years, the limit would be ert, confirming the exponential growth of compound interest while giving us an upper bound on our earnings.)
Finally, you may recall from Calculus I that finding the slope of the tangent line at a point on a curve (that is, the derivative at that point) always produced an "indeterminate" form from the slope calculation,
In some cases, students (usually in high school calculus) who have seen l'Hospital's Rule try to apply it to these cases. For example, consider the limit,
that is the calculation of the derivative (tangent line slope) for the sine function at x = 0. Applying l'Hospital's Rule gives,
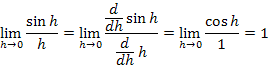
Although the answer is correct, obtaining it this way is "cheating" (that is, an incorrect application of l'Hospital's Rule)! Why? To use l'Hospital's Rule to find this limit, we must know the derivative of the sine function, but the derivative of the sine function is derived from this limit! Thus, we are "going in circles." In mathematics, this type of circular logic is called begging the question, which we will leave for discussion in a course about mathematical logic.