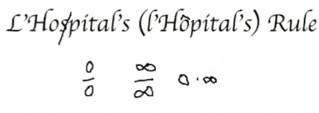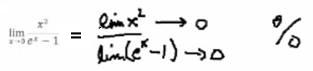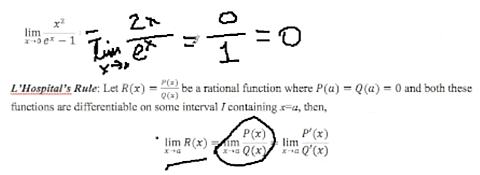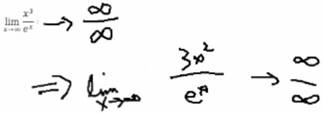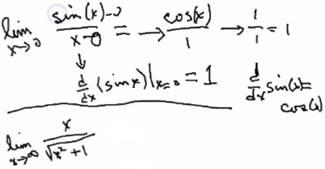L'Hospital's Rule

Somewhat steeped in controversy, l'Hospital's Rule was published by Guillaume de l'Hospital at the end of the seventeenth century, but the original idea was probably due to his academic advisor and later his financial beneficiary, Johann Bernoulli.

[Note that the lecturer uses the phrase indeterminable form, whereas most calculus texts use the more common phrase indeterminate form. The two are the same.]

In this lesson, I want to discuss l'Hospital's Rule, and it's spelled with a silent s (or, if you have the proper font set, with a carat over the o [ô]).

It is a rule to determine the limits when you have indeterminable forms—that is, when the limit of a rational expression goes to 0/0, or ∞/∞, or 0 ⋅ ∞, which you can rewrite in one of the previous forms.

So let's look at an example.

L'Hospital's Rule generally applies to situations where you have a rational expression. Recall from Calculus I, the limit of a quotient is the quotient of the limits, so I can take the limit of the numerator divided by the limit of the denominator.

If we look at each one of those as x approaches 0 [the numerator approaches 0 and the denominator approaches 0], we end up with the indeterminable form 0/0. This is undefined—you can't divide by 0, and 0/0 is undefined. This is called an indeterminable form.

L'Hospital's Rule gives us a method for solving these kinds of limit problems. He built on the work of Bernoulli, who first found this rule, so sometimes you'll see in the literature that this is called Bernoulli's Rule; but in fact l'Hospital did the main mathematics for it, so it usually bears his name.

Here is a statement of l'Hospital's Rule. This is covered in more detail in the Introduction section of this topic. But basically it says that when you have this kind of a rational expression that goes to 0/0, the limit on the quotient can be found by taking the derivative of the numerator and the denominator independently.

In other words, don't take the derivative using the quotient rule; take the derivative of the numerator only and take the derivative of the denominator only, and the limit for this fractional expression will be the same as the limit of the quotient of the derivatives.

So, take the derivative of the numerator, take the derivative of the denominator, and if the limit exists—and it may be that when you take these limits, you get another indeterminable form—but if the limit exists, it will be the limit of the original expression.

Let's try this on our example. We'll take the derivative of the numerator—that's 2x. The derivative of the denominator is e^x because the derivative of 1 is 0.

And again, I'll take the same limit—as x approaches 0. Now the numerator goes to 0, the denominator goes to 1, and so my overall limit is going to be 0.

In the beginning, I couldn't evaluate [the limit of the fraction]—it came out to be 0/0—but by l'Hospital's Rule, the limit is 0.

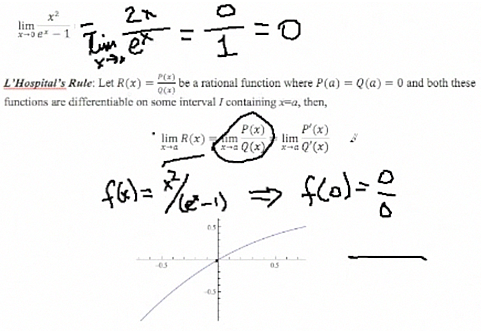
One quick way you can check this is to actually graph the rational expression, so I graphed the function that was in my limit: x²/(e^x − 1).

Notice that f(0) is undefined because it is also 0/0. But the limit, according to l'Hospital's Rule, is 0, so the limit exists, but we actually have a hole in the function.

The function is undefined [at x = 0]; it looks continuous, but we actually have a hole at zero.

So you can do a quick check, but you won't actually see the hole unless you have an infinite magnifying graphing program. But it is one quick way to check.

L'Hospital's Rule basically says that if you get an indeterminate form, take the derivative independently of the numerator and of the denominator, take the limits on those, and if the limit exists, that limit is the same as the original limit.

Let's consider another example where the limit is taken as x approaches infinity. You may remember from Calculus I that when we take the limit as x approaches infinity, we are really looking for horizontal asymptotes. The question here is, does this function have a horizontal asymptote?

Looking at this—we know that the limit of the quotient is the quotient of the limits—as x approaches infinity, x³ approaches infinity and e^x approaches infinity. So we have the interminable form ∞/∞, and we can apply l'Hospital's Rule: Take the derivative of the numerator, which is 3x², and take the derivative of the denominator, which is again e^x.

Take the limits again. Unfortunately, the numerator approaches infinity and the denominator approaches infinity, giving the indeterminable form ∞/∞.

We can apply l'Hospital's Rule again, and just keep going. The derivative of 3x² is 6x, and the derivative of the exponential e^x is e^x, and the limits of both go to infinity. So again, we have the indeterminable form ∞/∞ because both numerator and denominator go to infinity.

Apply l'Hospital's Rule again—just keep going until you recognize there is a problem or you end up with a limit.

The derivative of 6x is 6, so the numerator is a constant. That means you cannot apply l'Hospital's Rule again. You can only apply l'Hospital's Rule if you get an indeterminable form. Now this limit doesn't; it goes to 6/∞, which is 0. So there is a horizontal asymptote at 0.

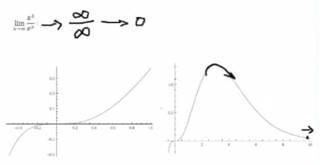
Again, I'm going to graph the rational expression function x³/e^x. You have to be careful, here, because here I've just graphed it from −½ to 1. It looks like it is increasing—which it is—because the numerator isn't dominating in this interval.

But what we are interested in when we are taking the limit as x approaches infinity, is what is happening when x gets large.

So let's make a graph of that. I've graphed the function out to x = 10. You can see that the function has turned around and headed back down. In this region, the exponential e^x is starting to get bigger; and farther out, it begins to dominate.

I have one more graph here, where x goes out to 20. You can see that it is asymptotic at 0.

A graph is not a proof. A graph is simply an indicator that you are correct.

The actual proof that this goes to 0 is the application of l'Hospital's Rule.

In the examples in the Introduction to this topic, we show that no matter what the polynomial x^N is, the exponential e^x will eventually dominate, and the limit will approach 0. You will have a horizontal asymptote at 0 for any polynomial in the numerator divided by e^x. The exponential always grows faster than any polynomial. See the Step-by-Step Examples section for complete details.

In closing, I want to mention a couple of cases that are covered in more detail in the Introduction and Step-by-Step Examples sections, where l'Hospital's Rule essentially fails.

Some students in Calculus I look at the limit of sin(x)/x and, having seen l'Hospital's Rule before, apply the derivative of sin(x) to get cos(x) and the derivative of the denominator to get 1. They take the limits on these, and get the right answer, which is 1/1, so the limit approaches 1.

Unfortunately, this is not correct. To actually evaluate the limit of sin(x)/x, this limit was used to determine the derivative of the sine function. It is the slope formula for the derivative of the sine at x = 0.

From finding that limit, using some specialized theorems in geometry and the squeezing theorem, we found the derivative of sin(x)/x at x = 0 was 1 (the slope of the tangent line), and we used that to find that the general derivative of the sine is the cosine. So we're using a circular type of logic, and l'Hospital's Rule shouldn't be applied in these cases.

This next case is covered in the Step-by-Step [Explanation] examples. When we apply l'Hospital's Rule repeatedly, we always end up with an indeterminable form, ∞/∞. So you need to find some other way to do this. You can use a standard Calculus I method.

L'Hospital's Rule is a powerful tool—and it is just that—particularly for asymptotic behavior, which we are interested in for a lot of problems that need to know what happens in the long term.

But don't just blindly apply l'Hospital's Rule. Make sure you examine the problem. A graph can help, but remember [that] a graph is not a proof.