L'Hospital's Rule
Summary
When taking a limit of a rational function (a quotient), the limit rule—stating that the limit of a quotient is the quotient of the limits—applies. However, if the limiting quantities of the numerator and denominator result in an undefined result, such as 0/0 or ∞/∞, the limit is said to be "indeterminate." In such cases, l'Hospital's Rule may provide the result.
L'Hospital's Rule is stated as follows:
Let 
be a rational function where P(a) = Q(a) = 0, and both of these functions are differentiable on some interval I containing x = a; then,
provided that the limits exist.
Note, however, that this rule does not apply whenever the numerator or denominator has a nonzero (finite) limit. The rule does apply if the indeterminate form is ∞/∞ and if a approaches ∞.
For example, when finding the limit
the numerator and denominator each approach zero as x → 1. Because the functions in the numerator and denominator are each differentiable, we can apply l'Hospital's Rule. Note that when applying l'Hospital's Rule, the derivative of the function in the numerator and the derivative of the function in the denominator are taken separately, and the quotient rule for differentiation is not used. Applying l'Hospital's Rule to this limit gives,
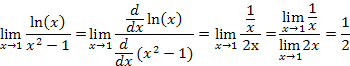
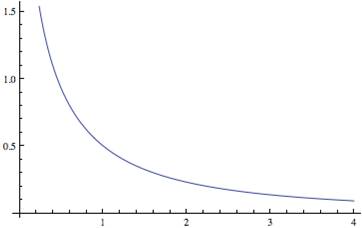
Graphing the rational function 
shows what appears to be a continuous function at x = 1. However, our result above shows that the limit exists but the functional value R(1) does not, so the function is not continuous at x = 1. If we define the function to be ½ at x = 1, the result would be a continuous function on the interval (0,∞)—that is,
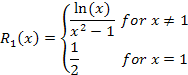
is continuous for all positive x values.
Figure 1
Graph of R1(x) on the Interval (0,4)
L'Hospital's Rule also works for indeterminate forms of the kind 0 ⋅ ∞. For example, find the limit,
First, we note that the 
is not defined for x < 0; thus, this (two-sided) limit does not exist. Instead, let's consider,
As x → 0, ln(x) approaches −∞. Thus, our limit is the indeterminate form 0 ⋅ ∞. To apply l'Hospital's Rule, rewrite the limit as,
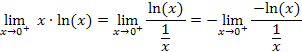
This latter limit is of the indeterminate form ∞/∞. Applying l'Hospital's Rule gives,
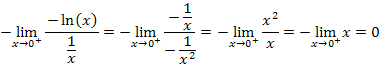
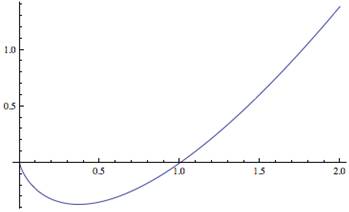
Thus, the one-sided limit exists and is zero. This can also be seen in the graph shown in figure 2 (but remember that a graph is not a proof).
Figure 2
Graph of x ⋅ ln(x) on the Interval (0,2)
Recall from the Introduction and Step-by-Step Explanation solutions that l'Hospital's Rule doesn't solve the limit of every indeterminate form. Used wisely, however, it can be a powerful tool in your mathematical arsenal.