Taylor Polynomials and Series
Step-By-Step Explanation
Example 1: Find a Taylor polynomial that will calculate the sin(x) for any input x to within an error of 0.000001 (one millionth).
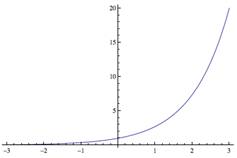
Example 2: Find the Taylor series for f(x) = e−x directly and by using the series expansion of f(x) = ex (about x = 0).
Example 3: Find an approximation of the number e to within 0.0000001 (one ten-millionth).
Example 4: Show that the series for ex converges at every value of x.
Example 1
| Figure | Problem | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Find a Taylor polynomial that will calculate the sin(x) for any input x to within an error of 0.000001 (one millionth). |
|||||||||||||||||||||||||||
| Step | Equation | Explanation | ||||||||||||||||||||||||||
1 |
|
The Taylor polynomial of order (not degree) n approximating a function f(x) is given by the formula at left. Notice that the polynomial is a function of x but also depends on the (fixed) point of expansion x = a. The point x = a should be chosen so that functional and derivative values are known at that point. |
||||||||||||||||||||||||||
2 |
|
The error between the polynomial and the function is given by the difference between the actual functional value and the polynomial value. Because the functional value is not actually known (that's why we are trying to estimate it!), the Taylor Remainder Formula (given at left) can be used to determine error estimates. |
||||||||||||||||||||||||||
3 |
|
In addition, using the symmetry and periodicity of the sine function, we only need to know the values on the interval [0, π/2] to determine the sine values for all the real numbers. Thus, let's expand sin(x) on [0, π/2] to the desired error. |
||||||||||||||||||||||||||
4 |
|
The Remainder Theorem states that a result at x would be exactly known if the value of c (a < c < x) were known. Examining the "worst case" selection of the value c will lead us to an error estimate such that the estimates will be within the error of the actual function values. |
||||||||||||||||||||||||||
5 |
|
The nth derivative of sin(x) is either a positive or negative multiple of the sine or cosine. The largest value attained by these functions is 1. So no matter what the value of c, 1 is the largest value this (derivative) term could be. |
||||||||||||||||||||||||||
6 |
|
In addition, because we only need approximate values on the interval [0, π/2], the largest value that (x − a) could be is π/2, because a = 0. |
||||||||||||||||||||||||||
7 |
|
Thus, the largest the remainder could be is |
||||||||||||||||||||||||||
8 |
Find n such that
|
To solve the problem, we must find the error estimate for each value until we find an n value where the error is less than the specified error (0.000001). |
||||||||||||||||||||||||||
9 |
Do loop |
This is, of course, a tedious calculation to do by hand; but if you are a programmer, you may realize that this is just a for or while loop with the condition to stop once the error limit is reached, as seen in the pseudocode at left. |
||||||||||||||||||||||||||
10 |
|
We can also do this calculation using a programmable calculator or a spreadsheet like Excel. |
||||||||||||||||||||||||||
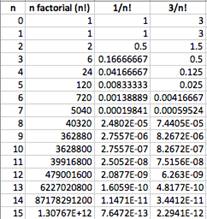
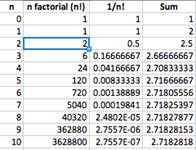
11 |
|
Let's use Excel to generate a table of error values. Recall that you can apply a formula to a cell, and then apply it to several cells by dragging the lower-right corner of the cell. |
||||||||||||||||||||||||||
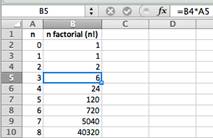
12 |
|
Here, 1.570796327 was used to approximate π/2. |
||||||||||||||||||||||||||
13 |
|
Our table shows that for n + 1 = 12, the error is 4.71087E-07 < 0.0000005 < 0.000001. Thus, taking n = 11 will generate an approximation within our error bound. |
||||||||||||||||||||||||||
14 |
p11(x) =
|
Calculating the p11(x) Taylor polynomial for the sin(x) about x = 0 gives the result shown at left. |
||||||||||||||||||||||||||
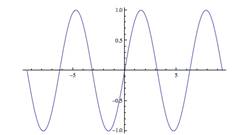
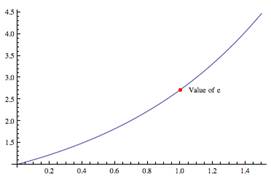
15 |
|
A graph of p11(x) with sin(x) shows them to be almost indistinguishable well beyond π), but our calculations have shown that we can use this approximation to calculate any value of sin(x) to within an error of less than a millionth. |
||||||||||||||||||||||||||
Example 2
| Figure | Problem | |
|---|---|---|
|
Find the Taylor series for f(x) = e−x directly and by using the series expansion of f(x) = ex (about x = 0). |
|
Step |
Equation |
Explanation |
1 |
|
As with the expansion of ex, it is a matter of finding and evaluating the derivative. Our only concern here is properly handling the negative sign from the exponent (an application of the Chain Rule). |
2 |
|
Repeating the process shows the pattern. |
3 |
|
Thus, we can write a general formula for the derivative. |
4 |
Thus, |
Substituting into the Taylor Expansion Formula gives our result (expanding about x = 0). |
5 |
Substituting −x for x,
|
Using the expansion of ex (about x = 0) and replacing x with −x gives the same result. |
Example 3
| Figure | Problem | |
|---|---|---|
|
Find an approximation of the number e to within 0.0000001 (one ten-millionth). |
|
| Step | Equation | Explanation |
1 |
|
Because (the number) e can be written as e = e1, we just need to evaluate the exponential function at x = 1, or equivalently, its Taylor expansion. Thus, the proper Taylor polynomial evaluated at x = 1 will give us the approximation we seek. |
2 |
|
As in Example 1, we use the Remainder Formula to approximate the error for ex on the interval [0, 1]. Because the function ex is strictly increasing, the maximum error will occur at x = 1. |
3 |
|
Once again, we are left with an estimate (which would be exact if we knew c and the value of e) in terms of the value we seek, as well as the unknown value of c (between 0 and 1). So the largest remainder would be for c = 1. |
4 |
|
Although we don't know the value of e, we do know from the Intermediate Value Theorem that 2 < e < 3, so in particular, e < 3, which we can use to bound our error. |
5 |
|
Thus we need to find n such that our estimate is less than the desired error. |
6 |
|
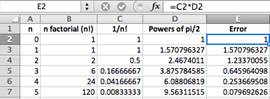
As in Example 1, we generate a table using a calculator or Excel or a similar spreadsheet. |
7 |
|
From the table, we see that for n + 1 = 11, the error is less than our desired value of 0.0000001. |
8 |
|
Thus, we need to calculate p10(x) for the function ex; that is, truncate the series for n = 10. |
9 |
|
This sum can be evaluated using a calculator, but that would be tedious; so again, go to Excel or a programmable method. Our estimate, then, is 2.7182818. |
10 |
|
Checking this estimate on a calculator (or a more accurate estimation method), we see that the error is 0.0000000285… < 0.0000001. |
Example 4
| Figure | Problem | |
|---|---|---|
|
Show that the series for ex converges at every value of x. |
|
| Step | Equation | Explanation |
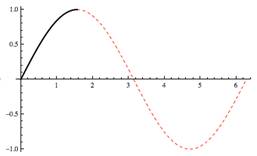
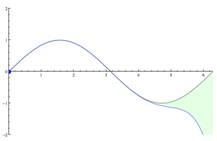
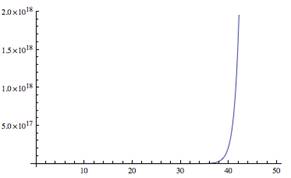
1 |
In the graph above, we see that the values of the exponential function are so "small" on a plot over the range [0, 50] that they appear to be zero (that is, they lie on the x-axis). |
There are several tests for convergence—root test, ratio test, integral test, etc.—see the textbook for a statement of each. The question is, as the values of x get large, so do the values of the Taylor expansion. And the values of the function ex get really large! So do these values (the function values and the Taylor explansion value) start to diverge, that is, does their difference (separation) get larger than some small specified error ε as the values of x get large? |
2 |
|
We have seen in the previous examples that the Taylor series, as given at left, attains a small error quite rapidly for values of x less than (for example) 10. But does this hold for all x? |
3 |
|
The Ratio Test is one of the easiest to apply, so let's see if it works here. The limit of the ratio is shown at left. |
4 |
|
Although our result depends on x, the limit is strictly in terms of n. Thus, for any x value, n eventually gets large—in fact, much larger, and the ratio |
5 |
In particular, for x = 1,000,000,000:
|
For example, if x were a billion (try finding e1,000,000,000 with your calculator!), once n, on its way to infinity, gets to a billion also, then the ratio is less than one. Taking n in steps of a billion (after all, that's still small compared with infinity), we can see that for n equaling one billion, two billion, three billion, and so on, the ratio is less than one, one-half, one-third, and so on, and so goes to zero as n → ∞. Thus, the series converges for all values of x! |
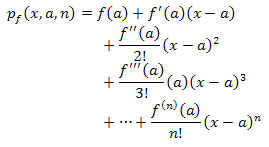
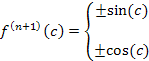
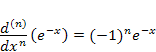
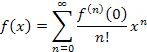
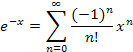
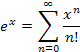
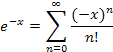
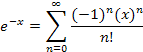
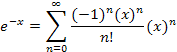
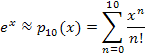
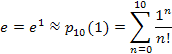
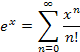
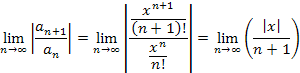
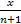 is small.
is small.