Taylor Polynomials and Series

• Introduction
• Video
• Video Transcript
• Step-by-Step Explanation
• Summary
• Exercises
• Return to Calculus II Topics

Taylor Polynomials and Series

Summary

We have seen that Taylor's methods allow us to approximate functional values, even for difficult transcendental functions like the exponential or trigonometric functions. So, suppose you want to build a calculator that can compute the values for a variety of functions, including transcendental functions like the sine, cosine, exponential, and logarithmic functions. Because basic calculators do addition (by adding clock cycles) and multiplication (by adding the same values very quickly) extremely well, polynomial values can be calculated rapidly. By their nature, transcendental functions cannot be represented by polynomials. As we have seen, however, they can be approximated by polynomials as accurately as desired. Furthermore, in many instances they can be represented by an infinite (power) series.

For example, let's calculate the sixth-order Taylor polynomial for the sine function about the point x = 0 (that is, a = 0 in the Taylor formula). An expansion about x = 0 is also called a Maclaurin expansion.

To do this calculation, we can use the Taylor expansion of the function sine as calculated in Example 1 of the Step-by-Step Explanation. So, the sixth-order Taylor polynomial about x = 0 for the sine is

Note that this is the sixth-order Taylor polynomial, although it has degree five. Graphing the polynomial with the sine function indicates a good approximation, at least close to the expansion point of x = 0. But for our calculation, what is the error in this approximation for all values of the sine function? Figure 1 compares the polynomial p₆(x) with the sine function. Using the periodicity and symmetry of the sine function, we only need our polynomial p₆(x) to be a good approximation on the interval [0, π/2], so let's check the error on this interval.

Figure 1
Graphs of the Polynomial p₆(x) and the Sine Function

 

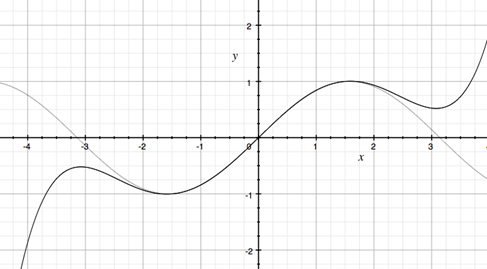
The error is given by the Taylor Remainder Formula, which for the sine function is given by

where c is some value between 0 and x. So what value should we use for the c? Because all sine values can be determined from the values on the interval [0, π/2], and because the error between the polynomial and the sine function is increasing as x increases (that is, the farther we move from the expansion point at x = 0), take x = π/2. Because the remainder will be largest when the cosine is greatest, take c = 0 to calculate the error. This will provide all the sine values needed and tell us the maximum error. Thus, the error is

That is, using the Taylor polynomial p₆(x) will approximate any value of the sine function in our calculator to within five thousandths.

For example, the sin(1) is, according to the numerical methods of Mathematica, equal to 0.84147098480789650665 (first 20 decimal places). The Taylor approximation we have derived gives

This is a difference of less than 0.0002 (actually, 0.00019568). So we could use the fraction  as a close approximation to the sine of one radian. Note that this was done by simply matching the function value and the first six derivative values (five, actually, because the sixth derivative value is zero) of the sine at the single point x = 0.

In summary, the steps to find the Taylor polynomial of order n to approximate a function f(x) are as follows:

1. Determine the expansion point x = a. This is a critical step because the function and derivative values will need to be known (not approximated!) at this point.

2. Determine the derivatives of the function to the necessary order N.

3. Evaluate the derivatives and polynomial coefficients.

4. Write the Taylor polynomial. As a check, if possible, graph the polynomial against the function.

5. Use the Remainder Formula to do an error analysis if it is needed.

As a final example, let's find the Taylor series for e^x and use it to approximate the value of the transcendental number e. Because we want to write an infinite series, it is, of course, impossible to find and evaluate all the derivatives of the function. Thus, we seek to determine some pattern so that we can evaluate the coefficients.

A known property of the exponential function is that it is its own derivative—in fact, this is how the value of the base e is defined! Also, no matter what the base, a⁰ is defined as 1. These two properties can be used to determine the evaluation of the derivative of e^x to any order.

Evaluating at x = 0, the derivative values will always be 1, that is, .

Therefore, the Taylor series expansion for e^x becomes

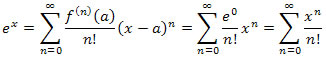
Note that the series index starts at n = 0 (which is the function evaluation) and that 0! = 1 by definition, so this first term is properly defined. Although it may not look like it at first glance, due to the powers of x, the series converges for any given x values (thus, for all x) due to the overwhelming growth of the factorial.

Note that this series can be used to get an approximation to the transcendental value e. Evaluating the series at x = 1 gives

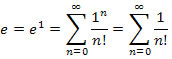
The Remainder Formula can provide an estimate of the possible error:

where c is some value between 0 and 1. Because the exponential is an increasing function, the maximum error estimate would occur when c = 1; but this gives an error estimate in terms of e, whose value we don't know. However, we do know that e < 3 (in fact, using the Intermediate Value Theorem, we know that 2 < e < 3). Thus,

The following table, generated in Excel, shows that the factorial grows very rapidly and the error can be bounded to a low estimate for a reasonably small n value.

N Value	Factorial	Error Estimate
1	1	3
2	2	1.5
3	6	0.5
4	24	0.125
5	120	0.025
6	720	0.004166667
7	5040	0.000595238
8	40320	7.44048E-05
9	362880	8.2672E-06
10	3628800	8.2672E-07
11	39916800	7.51563E-08
12	479001600	6.26303E-09
13	6227020800	4.81771E-10
14	87178291200	3.44122E-11
15	1.30767E+12	2.29415E-12
16	2.09228E+13	1.43384E-13
17	3.55687E+14	8.43437E-15
18	6.40237E+15	4.68576E-16
19	1.21645E+17	2.46619E-17
20	2.4329E+18	1.2331E-18

 

The table shows that an error of less than a millionth can be achieved with n = 10, thus,

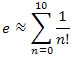
Turning back to Excel (or any calculator that can be programmed to do loops), a table can be quickly generated:

Because the right column is formatted to seven decimal places, the estimate value does not change for N greater than 10, as expected (why?); thus, our estimate for e is 2.718286, which is actually within one-millionth to six decimal places.

Return to top.