Taylor Polynomials and Series
Introduction

The transcendental number pi (π) is easy to define but hard to calculate. Pi is the ratio of the circumference of a circle to its diameter (π = C/d), but as a (transcendental) irrational real number, it is a nonrepeating, nonterminating decimal and thus can never be written exactly using a finite notation. The value of π has intrigued mathematicians for ages.
The ancient Greek mathematician Archimedes was one of the first to approximate π to several decimal places by successive approximations, using inscribed and circumscribed polygons.
Click the Play button to see how these inscribed and circumscribed polygons approach a circle as the number of sides increases. We begin with an inscribed and circumscribed square. Note how the value of pi approaches 3.14159 as the number of sides increases.
Figure 1
Archimedes's Approximation of pi
Over the years, many others refined these estimates, including the quickly converging estimates of John Machin. This was the "state of the art" that Brook Taylor discovered when he became a doctoral student of Professor Machin. Taylor went on to extend these ideas far beyond the estimates of the time with methods that became the basis for infinite series, analytic functions, and approximation theory. For his work, Brook Taylor later became a member of the Royal Society, and his results were named for him.
Before investigating Taylor's results in other sections of this topic, let us first define a few terms.
-
A sequence is a set of numbers indexed by the natural numbers (or whole numbers or integers). In notation, this is written as {an} where n, called the index, is a natural number (that is, n = 1, 2, 3, 4, … ). The index could also start at n = 0 (that is, the indexing set is the set of whole numbers), and some sequences are indexed using the integers (that is, the index may be positive, negative, or 0).
A sum or finite series is the sum over some finite range of index values of the terms of a sequence. We write a finite series as
We call the left side the sigma notation for a series; the right side is called the expanded notation.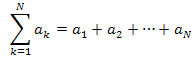
-
The value k is called the index and is defined by the upper and lower limits in the sum, which is indicated by the sigma notation, Σ. The index begins at the lower index value and continues increasing by one until it reaches the upper index value.
An infinite series (or simply series) is an infinite sum of all the terms of a sequence; that is,
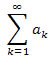
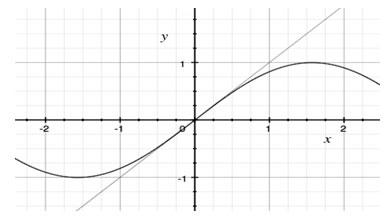
Taylor's desire was to approximate a given function using a finite or infinite series. To do this, he developed an idea that was the best of mathematics—simple to state yet rich in depth. The idea was to "match" the derivatives of the function at some point x = a. This idea is an extension of the concepts of calculus that the derivative of a function f(x) evaluated at x = a gives a linear approximation to the function for values "close" to x = a (see figure 2). The word close is enclosed in quotation marks because the error in this approximation will progressively increase as the function varies near the point x = a.
Taylor extended this idea by matching not only the first derivative, but also derivatives of higher order. This led to several central ideas, including the Taylor Polynomial, the Taylor Series, and the Taylor Remainder Formula.
The tangent line to a function (below, sin(x) with the tangent at x = 0) can be used as a linear approximation to the values of the function close to the point of tangency.
Figure 2
Tangent Line Used as a Linear
Approximation to the Values of Function sin(x)
Taylor's primary results are stated in the following theorem.
Recall that the notation n! is read as "n factorial" for n, a positive integer, and is defined as n! = (n) (n − 1) (n − 2) … (2) (1).
The expression
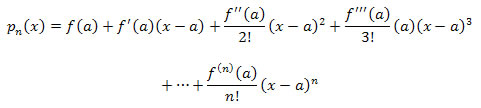
is called the Taylor polynomial about x = a of order n. (It is NOT "of degree n" because the nth-order derivative could be zero.)
The expression
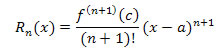
is called the Taylor Remainder Formula. Note that the value c is usually unknown—if it were known, we could identify f(x) exactly and would not need an approximation.
As an example, figure 3 shows the sine function graphed with a fifth-order Taylor polynomial approximation expanded about x = 0. (Note: A Taylor expansion about the point x = 0 is also called a Maclaurin expansion.) This expansion matches the first five derivative values of the sine function. As can be seen, the approximation is very close on the interval [0, π/2]. As we proceed through the lesson, we will see how this approximation and error are calculated.
Figure 3
Sine Function Graphed with a Fifth-Order
Taylor Polynomial Approximation Expanded About x = 0

The shaded green region represents the error between the approximating
Taylor polynomial (top curve) and the sine function (bottom curve).
