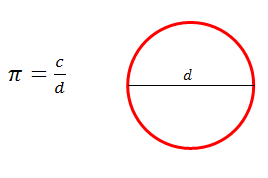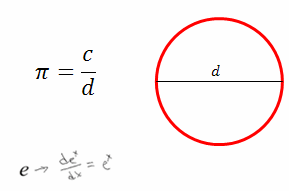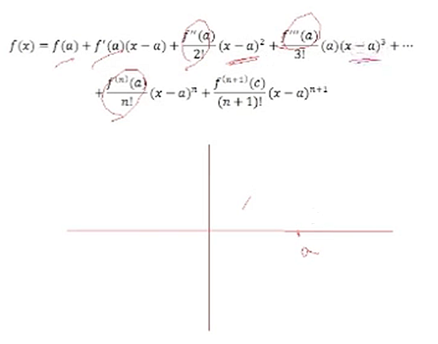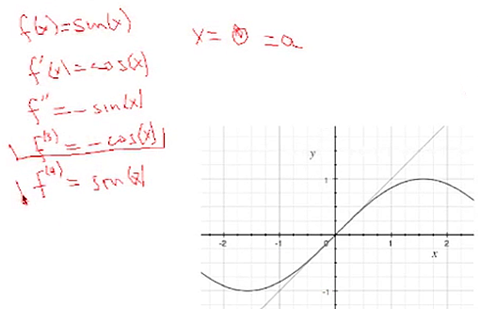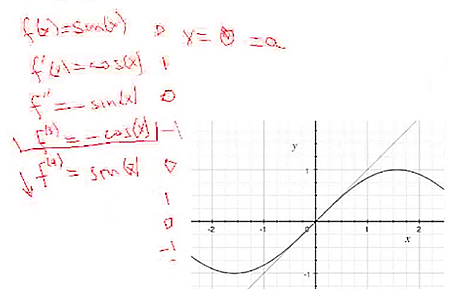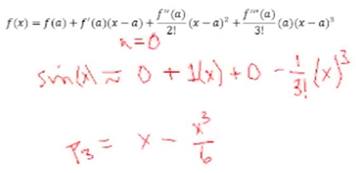Taylor Polynomials and Series

In this lesson, we want to talk about Taylor polynomials and the idea of infinite series, and mainly the idea of an approximation method of a function by a polynomial. In particular, we want to look at transcendental functions and how to approximate them with polynomials. It was really Brook Taylor who solved this problem.

But before we look at transcendental functions, let's do a little review of transcendental numbers.

One of the first transcendental numbers to be defined or discovered was the number pi. In ancient Greece, it was known, or defined, that the ratio of the circumference of a circle to its diameter was always the same number. This number was defined to be pi.

Although they didn't know what type of number pi was, it was later discovered to be a transcendental number. A transcendental number means that it is not the solution to an algebraic equation, so it is not the solution to a polynomial equation. And because it came up so often, a great effort was made to find an approximation for it.

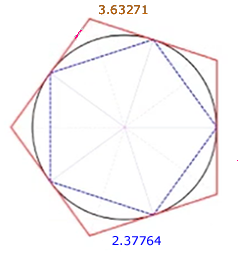
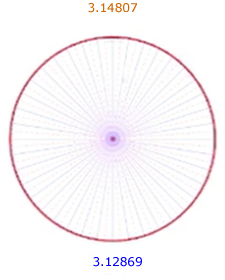
A transcendental number is an infinite, decimal, real number that never repeats, so the best we can do is try to get an approximation of it. So that effort [to find an approximation] went on for a while.

In the early days, Archimedes, an ancient Greek mathematician, tried ways of approximating it with polynomials. Archimedes used polygons around the circle, on the outside and inscribed, to try to approximate the value of pi.

By adding up all the sides of the polygon on the inside and outside, he was able to get bounds on the upper and lower values of pi, and he came out with a pretty good approximation, as you can see.

After a few iterations of this—actually [he used] a 40-sided polygon—he got a pretty good approximation. You can see that the value is between 3.128 and 3.148, and we now know it is 3.14159.

Another transcendental number, which was defined in Calculus I, is the number e.

Again, it wasn't known to be transcendental until the nineteenth century; but it was defined as the base number, so the derivative of e^x was itself.

So it was defined as that base that makes the derivative of the exponential function equal to itself. That turned out to be useful in a lot of natural growth and decay problems.

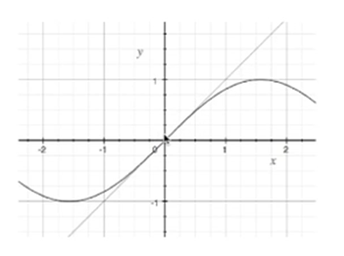
We want to look at how [pi and e] get approximated—in particular, what Taylor did in approximating functions by polynomials.

Recall from Calculus I that the derivative gives you the slope of the tangent line, and you can use that tangent line—here, we have the sine curve and the tangent at zero—to get an approximation of the function (at least in the close neighborhood) close around the value where the tangent point is.

Here the tangent is at zero, so you can see that the tangent line and the sine function are very close here.

What Taylor did was to say, instead of matching the functional value and the first derivative, let's match the second derivative, third derivative, fourth derivative, etc., and derive a polynomial based on that matching and see how well it can approximate the function on a wider range of values.

Here is a formula that Taylor came up with for the polynomial. He said, we've got an arbitrary function and we want to approximate a polynomial, so let's pick a point a, match the functional value at a—so we need to know the functional value, the derivative, the second derivative, the third derivative, and on up until the nth order. This is called an nth-order approximation.

We are going to expand about the point a, so the polynomial is written in terms of x − a.

We've got some function here and at the point (a, f(a)), we have to know the value of the function and its derivatives at that point, and we're going to have to match the first derivative, the second derivative, the third derivative, etc., up to the nth order.

The order may not be the degree because we don't know if a derivative may be zero, so we call it nth order instead of nth degree.

Taylor determined that the last term—the remainder—is what keeps this from being exact. The first part is the polynomial and the last term is the remainder.

So we are going to choose some point a, and we're going to match the functional values and the derivative values at that point up to some order n.

Taylor said that would be exact if we knew this remainder value. The remainder says that we need to know the nth derivative, the (n + 1)th derivative, at some point c that is between our x value and a. Here, we take an approximation, so we want to know the value of the function at that point.

The polynomial is going to [have] some error. The remainder, Taylor says, is exact if we knew some value c. But, of course, if we knew that, we wouldn't have an approximation anymore; we'd know the value exactly.

So [the remainder] is sort of unknown, but it can give us an estimate of the error. We want to use this remainder value function as an estimate for our error on the polynomial.

We're going to calculate the Taylor polynomial by this formula. Notice that factorials appear here. The factorials are [here] because the power rule on the derivative says that we're going to bring down the exponent. Every time we take the derivative of a polynomial, we bring down the exponent, so we get here 3 times 2 times 1. So n! is just n times (n − 1) times (n − 2), etc. Therefore, 6! = 6 times 5 times 4 times 3 times 2 times 1. We'll need that in our calculation.

Let's do a specific example. Let's look at the sine function. Here's the graph with the tangent line at 0. Let's expand at x = 0. Our a value is going to be 0, so we need to find the functional values and derivatives at 0.

The first derivative is cos(x). The second derivative is the derivative of the cosine, which is minus the sine (−‍sin(x)). The third derivative is −‍cos(x). The fourth derivative is sin(x).

Now notice something interesting. If I take the fifth derivative, I'm just going to start repeating this pattern again. Once I get the [first four derivatives], they are just going to repeat.

Now I just need to evaluate these at 0. So the evaluation [of sin(x) at 0 is 0, of −‍cos(x) is 1, of −‍sin(x) is 0, of −‍cos(x) is −1]. This pattern is just going to repeat: 0, 1, 0, −1, and so on.

Here is the third-order Taylor polynomial. We want to evaluate for the sine. The sine is going to be our polynomial approximation. Our third-order polynomial is

x – (x³/6).

Notice that it only contains odd powers of x, which is consistent with the fact that the sine is an odd function.

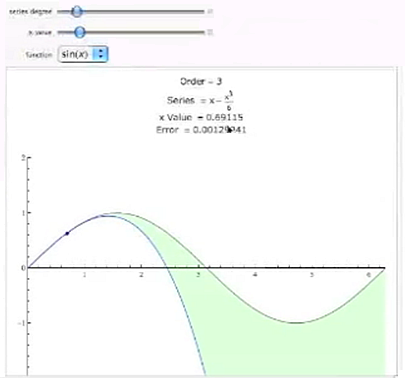
Here is a Mathematica demonstration that shows the sine curve and the polynomial. Our series is x − (x³/6). At zero, our error is zero because it is designed to match the value there. But if I [increase the x value], we can see that the error increases as x increases.

As I go to approximately pi/2, the error is a little less than 1/10—it's like 75/1,000. But that's not too bad, because I am only using a third-order polynomial. But we can program it into a computer pretty easily. All we need are the sine values from 0 to pi/2, and we could generate all the sine values by the symmetry and periodicity.

If I increase the degree—of course, if I go to the fourth degree, the next derivative is zero, so I really don't get anything more there—but as you can see, as I increase the degree, things get a lot better. Even at the 10th order, which is a ninth-degree polynomial, the error at pi/2 is only 27/10,000,000. That's really pretty good when we are at a ninth-degree polynomial. You notice that the denominators are getting pretty large because of the factorials.

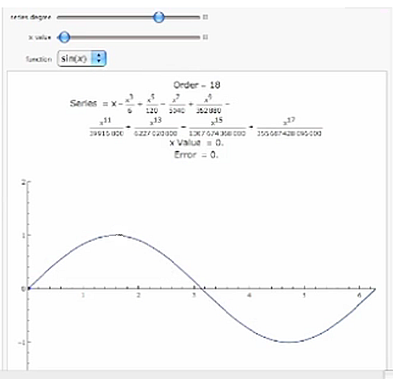
When I [take the degree] way up and actually match one cycle of the sine with a 17th-degree polynomial, I've got an error of less than 10 thousandths.

You can see that these Taylor polynomials can be very useful in approximating transcendental functions. They are very handy for programming into a computer or calculator to calculate the value of these functions quite accurately. This is one of their main applications.

To try to determine how big the error is, you need to use the remainder function (see the Step-by-Step Explanation of how that can be calculated). It's a little tougher problem because you have to specify the error, and then use the remainder function to try to get an estimate of that error, and figure out what degree polynomial you need to obtain that error.

Look at some of the other sections of this topic, and explore on your own.