Area Between Curves

Introduction
`Although Isaac Newton and Gottfried Leibniz are considered the founders of calculus, Bonaventura Cavalieri laid the foundation for the principles of modern calculus. A seventeenth-century Italian mathematician, Cavalieri was the first to formularize areas and volumes in terms of an indefinite number of infinitesimals, or small quantities. His work, along with the fundamental concept of a limit, was the foundation for modern integral calculus.
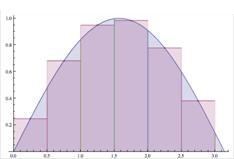
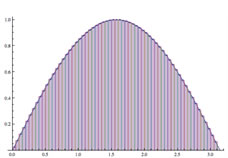
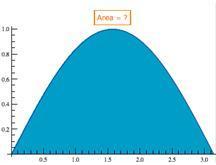
Recall from Calculus I that the area under the curve of a positive continuous function on an interval [a, b] is found from the limit of the sum of areas of approximating rectangles. Consider the approximations of the first "hump" of the sine curve shown below, in figure 1(a). Each rectangle has a length (height) of some value of the function, and a width of an increment (Δx) along the x-axis. As this width is made smaller (figure 1(b)), this approximation improves. Taking the limit as Δx→0, if this limit exists, it is defined as the definite integral,
![]()
and represents the area under the curve of the function (the blue area in figure 1(c)). Furthermore, it was shown that this limit, if it exists, is independent of the function value on the Δx subinterval chosen for the height, which can be the left endpoint, midpoint, right endpoint, and so on, of the rectangle.
Figure 1
Approximating Rectangles Approaching the Area Under the Curve
| (a) | (b) | (c) |
 |
 |
 |
The Fundamental Theorem then states that this definite integral value can be found by finding the antiderivative of f(x) and evaluating at the limits of integration; that is,
![]()
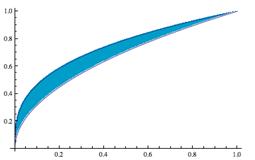
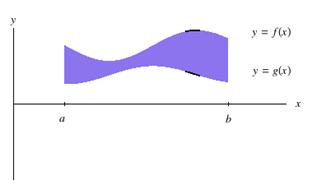
Figure 2 illustrates two examples of the areas between two curves.
Figure 2
Examples of Areas Between Two Curves, or Functions
 |
 |
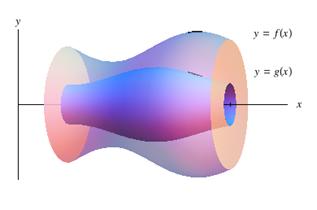
This problem has many applications, particularly in the generalization to volumes of rotations. Figure 3 is an example of an area between functions being rotated to generate a solid. For example, the volume of a sphere may be calculated from the rotation of a semicircular area around the x-axis. Calculating such volumes will be discussed in another topic.
Figure 3
Volumes Generated by the Rotation of an Area Region
 |
 |