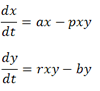Population Growth
Introduction

Depending on whose estimates you believe, the world population hit seven billion sometime between Halloween of 2011 (UN, 2011) and April Fool's Day of 2012 (US Census Bureau, 2012). You may think this is a trick because, just a decade ago, the population was six billion. Elizabeth Kolbert (2011) wrote a brief history of population growth in the New Yorker:
Depending on how you look at things, it has taken humanity a long time to reach this landmark, or practically no time at all. Around ten thousand years ago, there were maybe five million people on earth. By the time of the First Dynasty in Egypt, the number was up to about fifteen million, and by the time of the birth of Christ it had climbed to somewhere in the vicinity of two hundred million. Global population finally reached a billion around 1800, just a couple of years after Thomas Malthus published his famous essay warning that human numbers would always be held in check by war, pestilence, or "inevitable famine."
Of course, we all know that Malthus was off the mark; but as the world's population continues to increase (to perhaps 10 billion and growing by 2100), Kolbert has raised concerns about the planet's ability to sustain all that life:
As many, including Bill Gates, have pointed out, just to keep per-capita food production constant in the coming decades will require a second "green revolution." … Part of what made the first green revolution possible was a sharp increase in the use of phosphorus-rich fertilizers. Thanks to this increased use, experts say, reserves of phosphorus are now being exhausted. … Other essential commodities that could similarly run short include oil, water, and arable land.
In other sections of this topic, we will examine in detail three models of population growth: the exponential-growth model, the logistic model, and the predator-prey model. We briefly describe them below.
The Exponential-Growth Model
Given the growth in population over the past few decades and the fact that humankind has few predators, it seems reasonable to ask if human population growth is exponential. An unrestricted growth model (one that assumes no calamity like a famine that would impede the growth) postulates that the growth rate (derivative) is proportional to the size of the population P(t) at time t. This proportionality assumption results in the differential equation,
![]()
where k is the constant of proportionality.
The exponential-growth population model seems fairly accurate because people—with the exceptions of themselves, a few bacteria, and an occasional shark attack—have no real predators. Once a good "zombie virus" comes along, a predator-prey model may be more appropriate.
The Predator-Prey Model
Predator-prey models were presented in the mid-1930s by the great Russian mathematician Andrey Kolmogorov. He created models of two interacting populations (or species), where one was a predator, killing and perhaps feeding off another population, called the prey (the interaction of cheetahs and gazelles is a good example of this model). If two populations whose sizes at a reference time t are respectively denoted by x(t), y(t), then a general model of interacting populations may be written in terms of two autonomous (that is, time does not appear as an explicit variable) differential equations:
|
 |
where a and b are population-growth constants and the two xy terms model the interaction of the two species (controlled by constants p and r). Note that in the absence of these interactions (that is, p and r are zero), the model reduces to the standard population exponential-growth model discussed above.
The general predator-prey model is often called Kolmogorov's predator-prey model. Although there are several variations on this model, one of the most widely accepted is the Lotka-Volterra Model. Is such a model applicable to an unfriendly extraterrestrial invasion? Only the little green men know for sure, but a speculative model is developed and discussed in the Step-by-Step Explanation section of this topic.
The Logistic Model
 |
The human population, with no true predator, may be limited instead by resources—the size of the planet, ability to grow enough food, and so forth. These situations are best modeled by the logistic equation (sometimes called the Verhulst model or logistic growth curve), which is a model of population growth first published by Pierre Verhulst around 1845. The model is continuous in time and is described by the differential equation,
|
where r is the rate of maximum population growth (sometimes called the Malthusian parameter) and K is the carrying capacity—that is, the maximum sustainable population growth. This equation can be rewritten in the form,
![]()
where x is defined as ![]() . This equation is called the logistic equation and has the solution,
. This equation is called the logistic equation and has the solution,
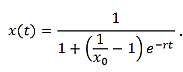
For this model to be applied to the world population, the carrying capacity and maximum growth rate r would need to be determined. We can probably assume that the growth rate will not increase and take r to be the growth rate determined from our exponential model. Estimating the carrying capacity is more difficult, however, because it requires predicting the future, which is where Malthus might have failed in his analysis. How many people can Earth support? Can technology supplement natural resources? What if man merges with machine, as Ray Kurzweil predicted in his book The Singularity Is Near? These are difficult questions to answer; but if we assume a carrying capacity of, say, 20 billion people, the model can be generated and checked over future generations.
With a carrying-capacity assumption of 20 billion, the model indicates that the population would reach 95 percent of that level in just over 200 years. The exponential-growth model predicts that the population level would be reached in under 60 years, using the same growth constant. Thus, the next generation should know which model to use for their predictions.
This scenario could change dramatically, however, if science fiction becomes science fact and extraterrestrials detect our radio signals and come searching for humans as prey. In that case, the predator-prey model of population levels may be more appropriate!
References
Kolbert, E. (2011, October 24). Comment: Billions and billions. The New Yorker. Retrieved from http://www.newyorker.com/talk/comment/2011/10/24/111024taco_talk_kolbert.
Kurzweil, R. (2005). The singularity is near: When humans transcend biology. New York: Penguin.
Malthus, T. (2012). An essay on the principle of population. Los Angeles, CA: Empire Books. (Originally published anonymously in 1798 through J. Johnson [London])
United Nations Population Fund. (2011). People and possibilities in a world of 7 billion. State of World Population 2011. Retrieved from http://www.unfpa.org/swp/.
United States Census Bureau. (2012). U.S. and world population clocks. Retrieved from http://www.census.gov/main/www/popclock.html.